LD-SODA: Lernbasierte Datenanalyse
Stochastik, Optimierung, Dynamik und Approximation
gefördert von der Landesforschungsförderung Hamburg der Hamburger Behörde für Wissenschaft, Forschung und Gleichstellung (BWFG)
Antragstellende Personen im kooperativen Forschungsverbund:
- Prof. Dr. Sarah Hallerberg (Sprecherin): Hochschule für Angewandte Wissenschaften Hamburg, Fakultät Technik und Informatik
Department Maschinenbau und Produktion - Prof. Dr. Armin Iske: Universität Hamburg, Fachbereich Mathematik
- Prof. Dr. Ivo Nowak: Hochschule für Angewandte Wissenschaften Hamburg, Fakultät Technik und Informatik
Department Maschinenbau und Produktion - Jun.-Prof. Dr. Mathias Trabs: Universität Hamburg, Fachbereich Mathematik
Motivation und Ziele
Maschinelle Lernverfahren, wie künstliche neuronale Netzwerke, Support Vector Machines oder Random Forests kommen im Rahmen der Digitalisierung in immer mehr Kontexten aus Wissenschaft, Technik und Gesellschaft zum Einsatz. Diese Verfahren zeichnen sich dadurch aus, dass sie unter sehr allgemeinen Modellannahmen funktionieren und prinzipiell mit sehr großen Datenmengen verarbeiten können, die dank moderner Mess- und Datenverarbeitungsmethoden verfügbar sind.
Jedoch ist typischerweise eine große Rechenleistung notwendig, um Lernverfahren in solchen Anwendungen zu nutzen. Um Risiken beim Einsatz von Lernverfahren zu reduzieren und um bestehende Algorithmen zu verbessern, besteht ein Bedarf an Verständnis und Nachvollziehbarkeit von automatisierten Entscheidungen. Die erfolgreiche Weiterentwicklung und Anwendung von Lernverfahren erfordert damit einerseits eine theoretische Fundierung dieser Verfahren und andererseits eine effiziente Implementierung. Aufgrund der Komplexität der Verfahren des maschinellen Lernens ist ein genaues Verständnis der Lernprozesse häufig noch nicht ausreichend gegeben.
Grundsätzliche Fragestellungen wie
- Wie kann man die Komplexität der Daten wirksam reduzieren?
- Welche Abhängigkeit von Ein- und Ausgabe können Lernmethoden beschreiben?
- Wie kann die zum Lernprozess nötige Optimierung effizient realisiert werden?
- Wie kann man die Dynamik des Lernprozesses verstehen und steuern?
- Welchen Einfluss haben Unsicherheiten und Störungen in den Daten?
führen auf mathematische Probleme aus unterschiedlichen Teildisziplinen.
Ziel dieses Forschungsverbundes ist es, maschinelle Lernverfahren in mathematischer Breite zu analysieren und auf dieser Grundlage, existierende Methoden zu verbessern, neue Methoden zu entwickeln sowie zu testen und so einen grundlegenden Beitrag zum maschinellen Lernen leisten. In Kooperation von Wissenschaftler*innen aus den zugrundeliegenden mathematischen Richtungen Stochastik, Optimierung, Dynamische Systeme und Approximation sollen in diesem Forschungsverbund folgenden wissenschaftliche Fragestellungen in Teilprojekten (TP) untersucht werden.
Teilprojekt TP-S: Support Vector Machines für statistische inverse Probleme
Verfahren des maschinellen Lernens kommen sehr erfolgreich in zahlreichen Anwendungen der Datenanalyse zum Einsatz, wobei typischerweise die Qualität der Verfahren anhand ihres Vorhersagefehlers gemessen wird. In fast allen Fällen handelt es sich um black box-Ansätze, es wird also nur die Abbildung von den Eingabedaten oder Features auf die Zielvariable betrachtet. Der Weg von der Eingabe zur Ausgabe bleibt weitgehend unklar.
In diesem Teilprojekt wenden wir maschinelle Lernverfahren auf inverse Probleme an und untersuchen deren statistische Eigenschaften. Genauer betrachten wir inverse Regressionsmodelle in denen die interessierende Funktion nicht direkt beobachtet wird, sondern nur deren Bild unter einem (linearen) Operator. Während die Vorsage durch das Vorwärtsproblem bestimmt ist und maschinelle Lernverfahren direkt anwendbar sind, muss für die Rekonstruktion der Zielfunktion der Operator invertiert werden. Solche inversen Probleme sind sowohl in der numerischen/deterministischen als auch in der statistischen Literatur detailliert studiert. Inwiefern maschinelle Lernverfahren angewendet werden können, ist jedoch weitgehend offen, da die erwähnte black box a priori einen Rückschluss auf die Zielfunktion erschwert. Unter den populären Verfahren des maschinellen Lernens konzentrieren wir uns auf kernbasierten Verfahren, insbesondere Support Vector Machines.
Project lead: Jun.-Prof. Dr. Mathias Trabs
Teilprojekt TP-O: Neue Column-Generation Algorithmen für tiefes Lernen
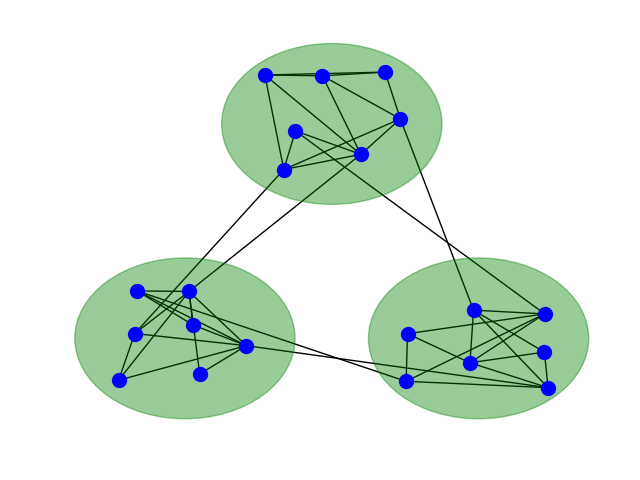
Foto: A. Iske
Hochdimensionale große Datensätze aus Anwendungen erfordern große künstliche neuronale Netze. Das Lernen mit solchen Netzen kann schwierig sein, da die hierfür erforderlichen Optimierungsprobleme groß, nicht konvex und nicht glatt sind. Zum anderen ist oft nicht klar, welche Netzwerkarchitektur, inbesondere die Anzahl der Netzwerkschichten und -komponenten, am effizientesten ist, da dies von den Trainingsdaten abhängt. Eine zu große Anzahl von Schichten kann zu Overfitting führen und eine zu kleine Anzahl kann die Approximationsgüte verschlechtern.
In diesem Teilprojekt entwickeln wir neue Column-Generation Algorithmen zur simultanen Bestimmung von optimalen Parametern und Architekturen von künstlichen neuronalen Netzen. Column-Generation Verfahren besitzen den Vorteil, dass ein durch innere Punkte definiertes Masterproblem generiert wird. Dieses bildet sowohl die Grundlage für die Bestimmung einer globalen und robusten Lösung, sowie für das adaptive Wachstum von neuronalen Netzen bzw. die Verteilung von Gewichten in Netzwerkkomponenten, wie z.B. bei modularen Mixture-of-Experts Architekturen (siehe Abbildung).
Projektleitung: Prof. Dr. Ivo Nowak
Teilprojekt TP-D: Dynamik und Störungsausbreitung in lernenden Netzwerken
Künstliche neuronale Netzwerke werden sehr erfolgreich zur Klassifizierung von Bildern und Geräuschen eingesetzt. Auml;hnliche Ansätze werden zur Zeit untersucht, um die Vorhersagbarkeit von Zeitreihen zu verbessern. Ziel dieses Teilprojektes ist es, den Prozess des Trainings einen künstlichen neuronalen Netzwerk als Dynamisches System zu beschreiben und zu verstehen. Die Dynamik besteht dabei aus der schrittweisen Auml;nderung der Gewichte des Netzwerkes und/oder in der zusätzlichen zeitlichen Dynamik der lernenden Einheiten. Dynamische Systeme lassen sich durch verschiedene Kenngröszlig;en und Methoden charakterisieren, wie zum Beispiel Angaben zur lokalen und globalen Stabilität. Insbesondere ist das Wachstum von Störungen sowie die Richtungen, entlang denen sich diese Störungen ausbreiten, interessant. Eine offene Frage ist, ob und wie sich der Lernprozess eines hochdimensionalen dynamischen Systems verändert (verbessert, beschleunigt), wenn man das System in einzelnen Lernphasen gezielt mit Störungen entlang dieser Richtungen beeinflusst.
Projektleitung: Prof. Dr. Sarah Hallerberg
Teilprojekt TP-A: Kernbasierte Approximationsmethoden zur adaptiven Datenanalyse
Leistungsfähige maschinelle Lernverfahren benötigen effiziente Methoden zur adaptiven Analyse sehr großer Datenmengen. In relevanten Anwendungen sind die (stetig wachsenden) Trainingsdaten typischerweise sehr kritisch, d.h. hochdimensional, heterogen verteilt, teilweise unvollständig und mit Unsicherheiten behaftet. Eine zuverlässige Analyse solcher Anwenderdaten erfordert problemangepasste und flexible Methoden der multivariaten Approximation, die jüngst mit geometrischen Projektionsmethoden der nichtlinearen Dimensionsreduktion verknüpft werden.
In diesem Teilprojekt entwickeln und analysieren wir neue Konzepte der kernbasierten multivariaten Approximation zur adaptiven Datenanalyse. Hierzu konstruieren wir problemangepasste Kernfunktionen, aus denen flexible und zuverlässige Werkzeuge zur Analyse kritischer Daten hervorgehen. Weiterhin entwickeln wir adaptive Algorithmen zur sparsen (d.h. dateneffizienten) Darstellung großer Eingabedaten. Bei der numerischen Analyse der daraus resultierenden adaptiven Algorithmen spielen relevante Aspekte der Komplexität, der Approximation und der Stabilität stets eine wichtige Rolle. Die Verknüpfung der kernbasierten Algorithmen mit modernen Methoden der Dimensionsreduktion erfordert die Charakterisierung topologischer und geometrischer Invarianzen, mit denen die Daten klassifiziert werden. Auf dieser Grundlage entwickeln wir neue nichtlineare Projektionsmethoden, die invariant unter den hier identifizierten (topologischen und geometrischen) intrinsischen Eigenschaften der Daten sind.
Projektleitung: Prof. Dr. Armin Iske
