Neues Advektions-Verfahren für geophysikalische Anwendungen

Das neue Verfahren ist ein explizites Verfahren mit zwei zusätzlichen Knotenpunkten in upstream-Richtung, so dass es global von 3.Ordnung ist. Lokal wird es umgeschaltet auf ein Verfahren 2.Ordnung, um Über- und Unterschwinger, die typisch für solche Verfahren sind, weitestgehend zu eliminieren. Die Rekonstruktion durch drei in upstream-Richtung gelegene Knotenpunkte erzeugt sehr grosse numerische Diffusion 4.Ordnung. Diffusion 4.Ordnung ist stark wellenzahlen-selektiv, d.h. es dämpft insbesondere die hohen Wellenzahlen. Obwohl das Verfahren frei von Diffusion 2.Ordnung ist, beobachtet man daher, dass scharfe Extrema stark gedämpft werden. Dagegen werden glatte Extrema, die auf mehreren Gitterpunkten repräsentiert sind, sehr gut widergegeben (siehe Beispiele unten). Das Verfahren besitzt im Gegenzug einen grösseren Stabilitätsbereich als übliche explizite Verfahren - die CFL-Bedingung (oder Courant-Zahl) darf zwischen 0 und 2, statt wie üblich zwischen 0 und 1, liegen. Dadurch lässt sich die Integrationszeit um etwa die Hälfte verringern. Der Umschaltmechanismus ist ähnlich zu solchen, die in WENO-Verfahren verwendet werden. Im Rahmen der Rechengenauigkeit ist das Verfahren massenerhaltend.

Im ersten Beispiel wird ein Rechteck-Signal mit einer Courant-Zahl von 1.5 nach rechts verschoben. Das Bild zeigt das Signal am Anfang (gestrichelt) sowie nach drei Umläufen durch das Gebiet mit periodischen Randbedingungen (rote Kurve). Das neue Verfahren erzeugt keine sichtbaren Über- und Unterschwinger. Die Verbreiterung des Signals entsteht durch die induzierte Diffusion 4.Ordnung, die bevorzugt hohe Wellenzahlen dämpft.

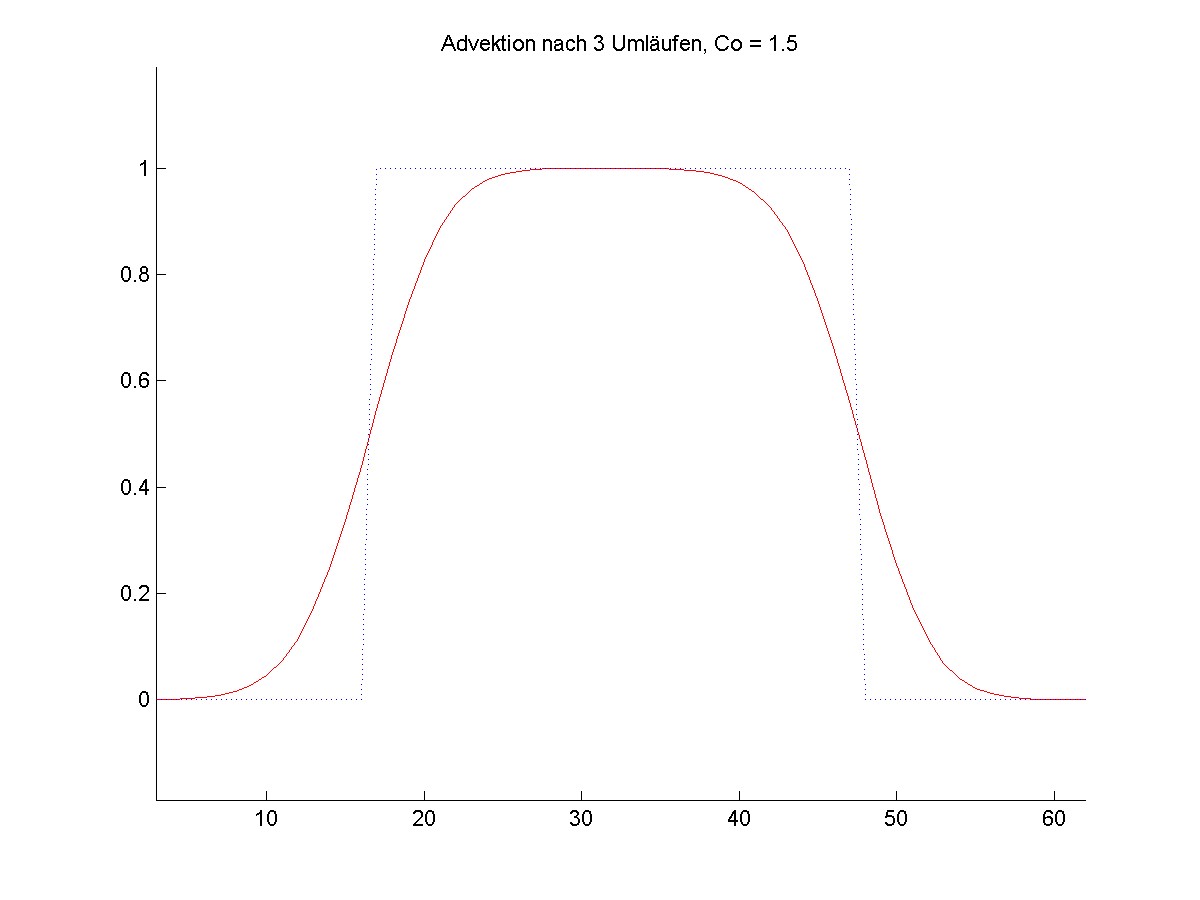
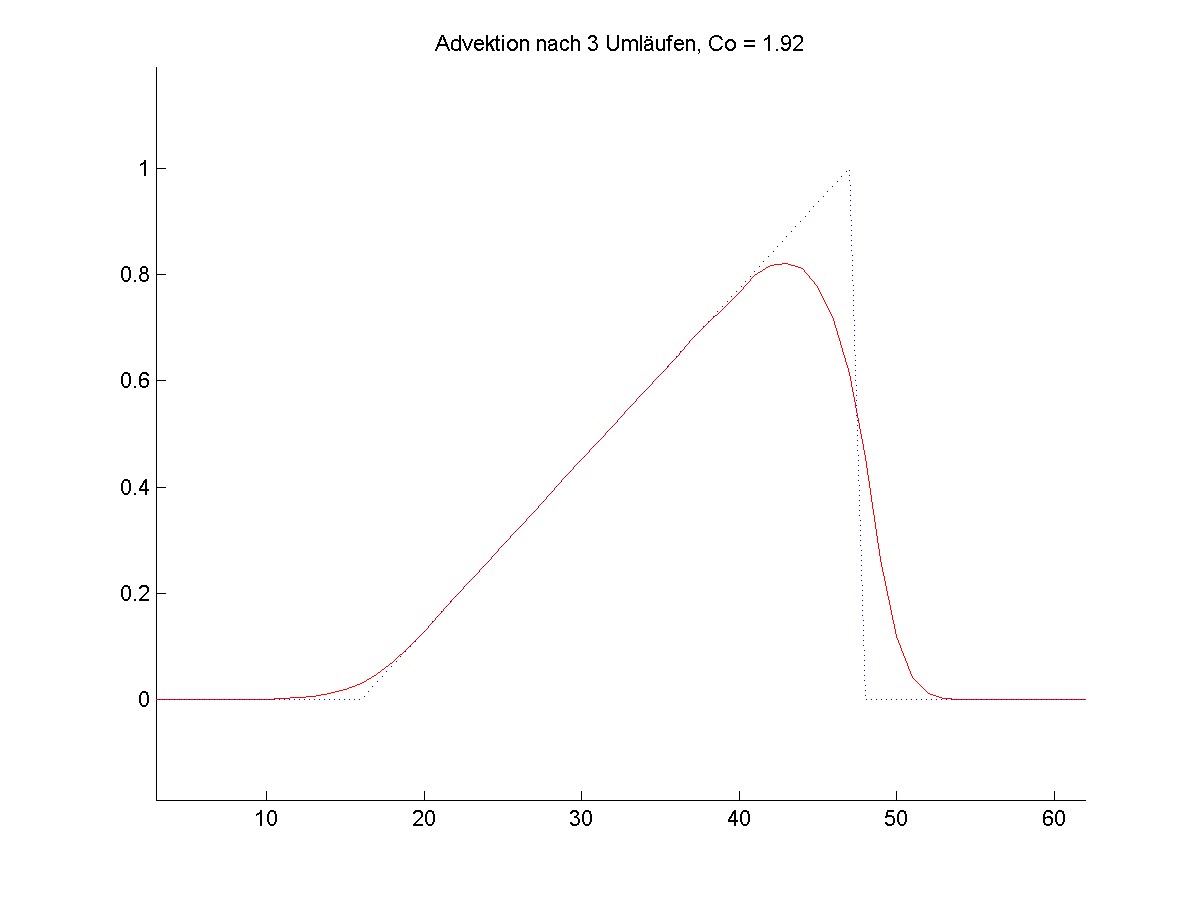
Die Advektion eines Dreieck-Signals verlangt vom numerischen Verfahren die Fähigkeit, asymmetrische Funktionen zu approximieren. Das neue Verfahren reduziert die Amplitude beträchtlich, ist aber wiederum oszillationsfrei. Hier zeigen sich die Schwierigkeiten mit scharfen Extrema, während das Extremum der Rechteckfunktion im ersten Bild problemlos erhalten wurde.

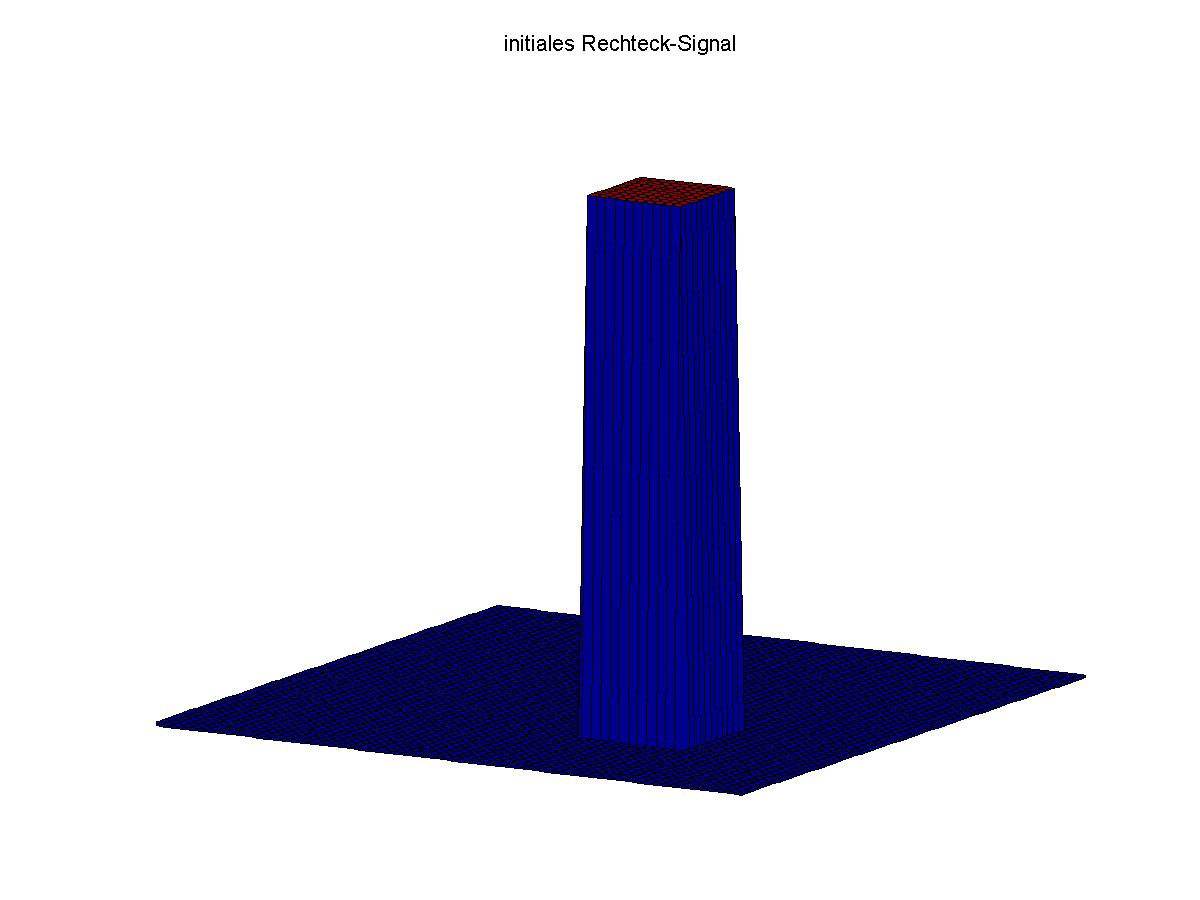
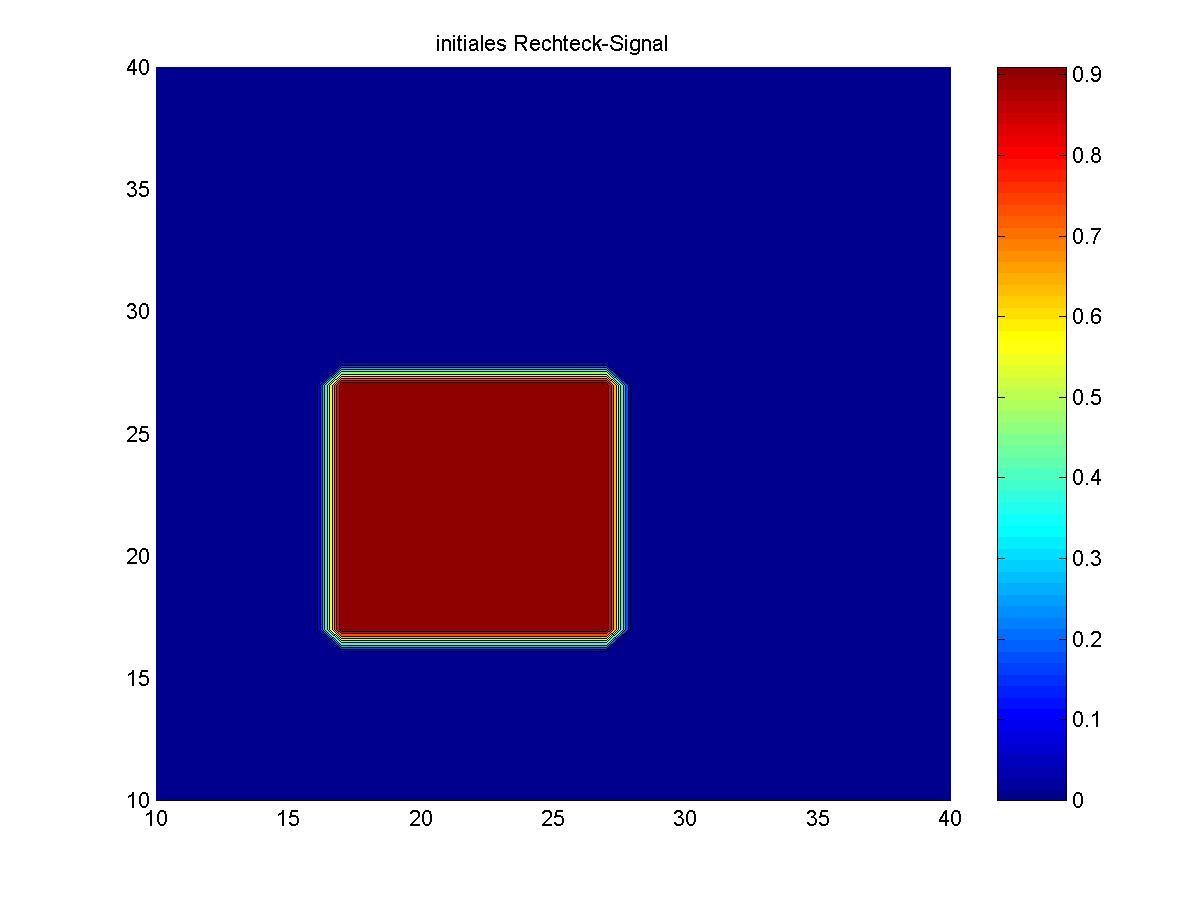
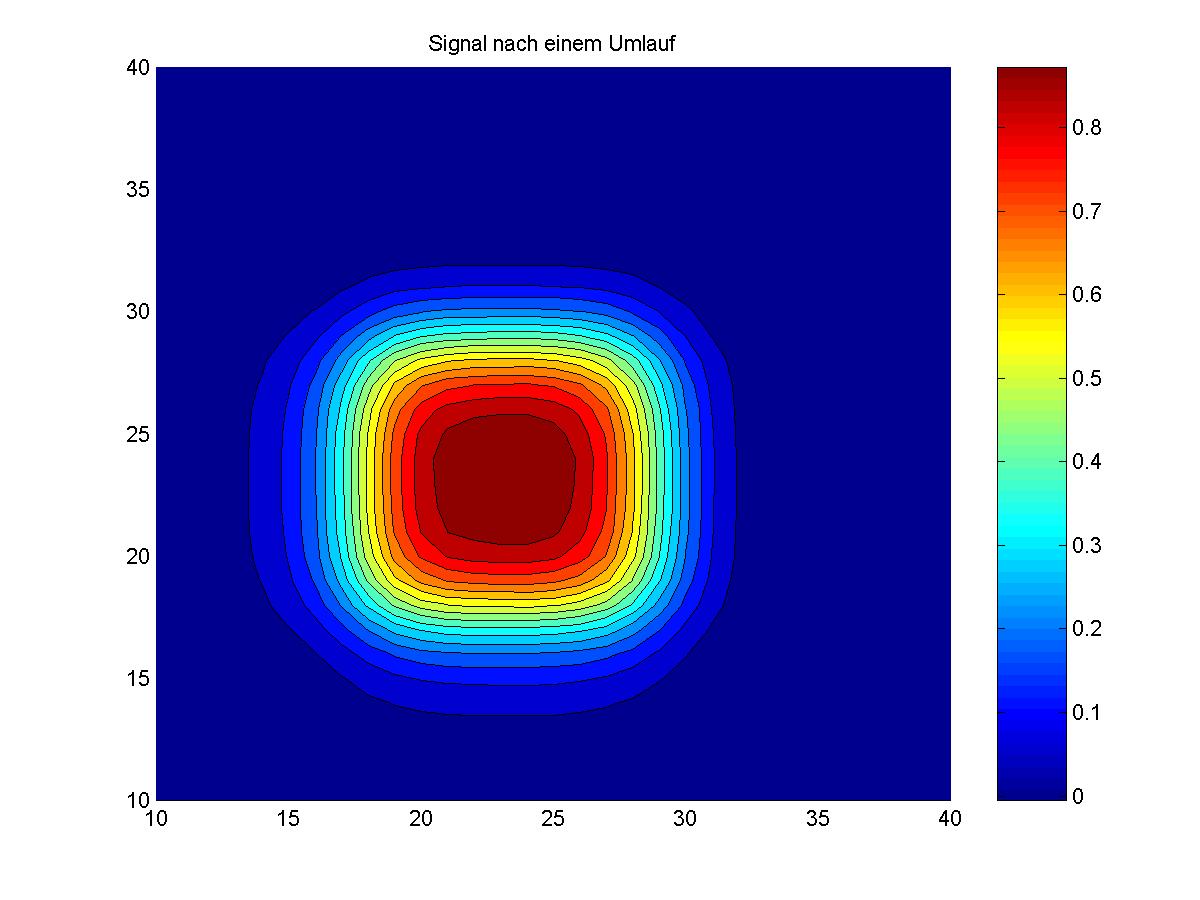
Auf den unteren Bildern ist die zweidimensionale Advektion eines Rechteck-Signals der Höhe 1 (links: Ausgangssignal, rechts: Signal nach einem Umlauf) dargestellt. Die Geschwindigkeiten in x- und y-Richtung betragen jeweils sqrt(2), so dass der Transport im 45°-Grad Winkel zum Gitter verläuft. Bei Ausbreitung quer zum Gitter zeigen sich bei vielen Verfahren unerwünschte Oszillationen, die mit (inhärent eindimensionalen) TVD-Methodiken nicht verhindert werden können. Das Signal bestreitet (fast) genau einen Umlauf durch das Gebiet mit periodischen Randbedingungen. Das hier benutzte neue Verfahren erzeugt Oszillationen, die mit blossem Auge nicht erkennbar sind (U_min = -0.0053) und erhält gleichzeitig das Maximum zufriedenstellend (U_max=0.9266).

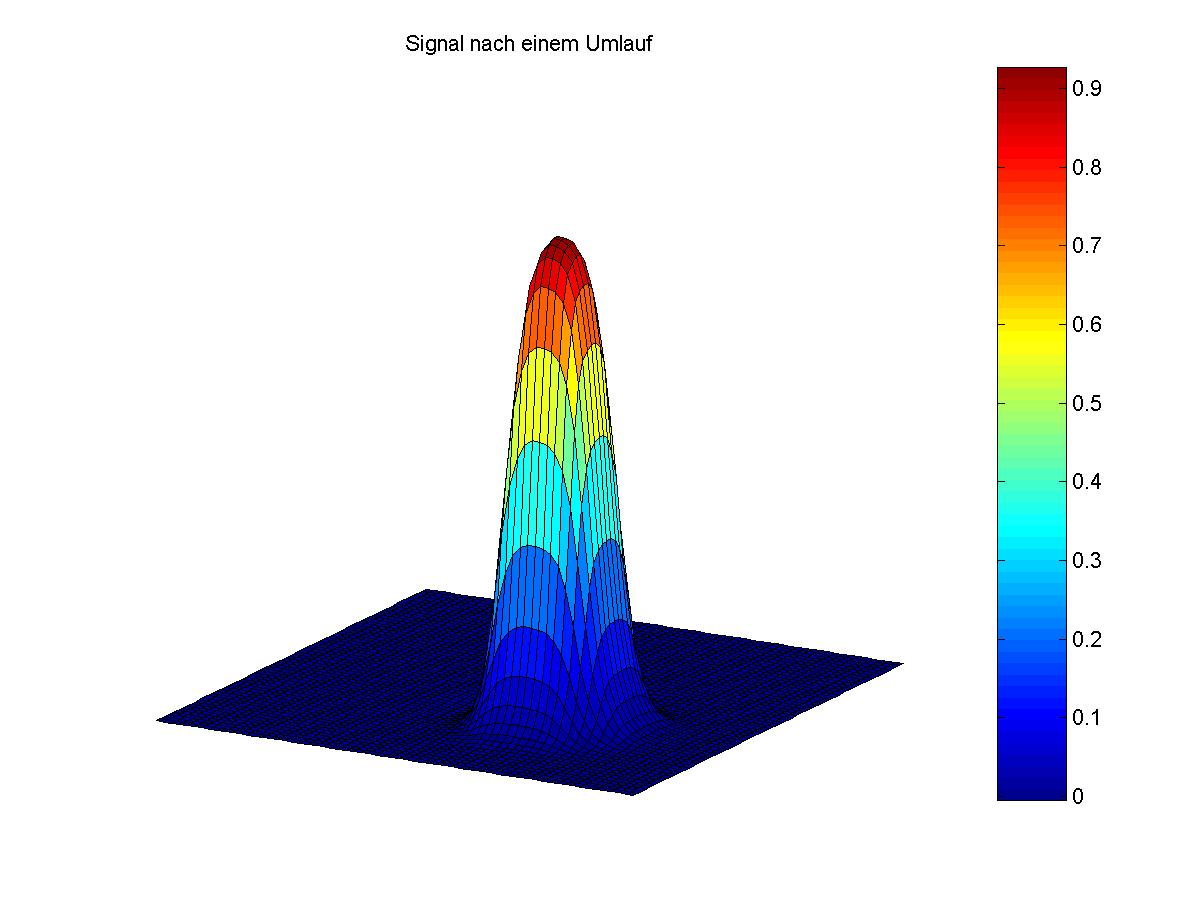
Ein Kontour-Plot zeigt zudem, dass die üblichen Verzerrungen, die in zweidimensionalen Problemen auftreten, hier weitestgehend vermieden werden. Stattdessen sorgt die Dissipation 4.Ordnung für eine Verbreiterung des Signals.

Der hier benutzte Algorithmus für die zweidimensionale lineare Advektion unterliegt der gleichen Zeitschrittbeschränkung wie das eindimensionale Verfahren (CFL <= 2) und ist global von 3.Ordnung, lokal von 2.Ordnung. Diese hohe Genauigkeit erfordert allerdings 2^d Schritte pro Zeitschritt, wobei d die Dimension des Problems ist. An Rechenzeit-sparsameren mehrdimensionalen Algorithmen (mit Verlust an Genauigkeit) wird zur Zeit gearbeitet.

zurück zur Projektseite