Stoffpläne
für die Lehrveranstaltungen der ersten Semester
Die folgenden Stoffpläne enthalten jene Inhalte aus den Bereichen
Analysis,
Lineare Algebra und Analytische Geometrie,
Numerische Mathematik und
Mathematische Stochastik,
die für das weitere Studium aller Studierender der Studiengänge
Mathematik, Wirtschaftsmathematik, Technomathematik und
Lehramt Oberstufen unverzichtbar sind.
Ziele der Beschäftigung mit diesen Inhalten sind gleichermaßen
- das Verständnis wichtiger Konzepte wie
- die sichere Handhabung grundlegender Techniken.
Gewicht gelegt werden sollte
- auf die Motivation neuer Fragestellungen,
- auf Veranschaulichung und Konkretisierung ebenso wie
- auf den Prozess des Abstrahierens,
- auf innermathematische Zusammenhänge,
- auf (möglichst auf die beteiligten Studiengänge abgestimmte) Anwendungsbezüge sowie
- auf Beispiele mathematischer Modellbildung.
Die konzeptionelle Aufbereitung sowie die Hinzunahme optionaler Inhalte
liegen in der Verantwortung des jeweiligen Veranstalters, soweit das Erlernen
der Stoffplan-Inhalte und die genannten Ziele und Gewichtungen nicht
gefährdet werden.
Analysis
Gegenstand der Analysis ist die Differential- und Integralrechnung einer
und mehrerer Veränderlichen. Zentral ist dabei der Begriff des Grenzwerts in
seinen verschiedenen Ausprägungen.
1. Semester
- Natürliche Zahlen, Induktionsprinzip.
- Reelle Zahlen: Eigenschaften (insbes.
Vollständigkeit), komplexe Zahlen.
- Folgen und Reihen reeller und komplexer Zahlen: Konvergenz, Konvergenzkriterien, Satz
von Bolzano-Weierstraß.
- Reelle Funktionen: Stetigkeit, Folgenstetigkeit, Zwischenwertsatz, Satz vom Maximum,
Grenzwerte von Funktionen, monotone Funktionen und Umkehrfunktionen.
- Elementare
Funktionen: Exponentialfunktion, Logarithmus, trigonometrische Funktionen und Arcusfunktionen.
- Differentialrechnung im
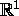 :
Linearisierung, Differentiationskalkül, Mittelwertsatz der Differentialrechnung,
Extrema, monotone und konvexe Funktionen. :
Linearisierung, Differentiationskalkül, Mittelwertsatz der Differentialrechnung,
Extrema, monotone und konvexe Funktionen.
- Integralrechnung im
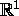 :
Riemann-Integral, Integrierbarkeit (gleichmäßig) stetiger Funktionen, Hauptsatz
der Differential- und Integralrechnung, Integrationskalkül, Mittelwertsätze. :
Riemann-Integral, Integrierbarkeit (gleichmäßig) stetiger Funktionen, Hauptsatz
der Differential- und Integralrechnung, Integrationskalkül, Mittelwertsätze.
2. Semester
- Integralrechnung im
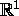 (Fortsetzung): Satz von Taylor, uneigentliche Integrale.
(Fortsetzung): Satz von Taylor, uneigentliche Integrale.
- Funktionenfolgen und -reihen: gleichmäßige Konvergenz, Weierstraßsches
Majorantenkriterium, Potenzreihen, Fourier-Reihen (Orthogonalität, Konvergenz im Mittel).
- Metrische/normierte Räume, insbesondere
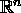 :
offene, abgeschlossene, kompakte Mengen, Konvergenz von Folgen, Banachscher Fixpunktsatz,
Stetigkeit bei Funktionen :
offene, abgeschlossene, kompakte Mengen, Konvergenz von Folgen, Banachscher Fixpunktsatz,
Stetigkeit bei Funktionen
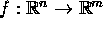 . .
- Differentialrechnung im
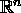 : partielle Ableitungen,
totale Ableitung (Jacobi-Matrix), Gradient, Mittelwertsätze, Taylor-Entwicklung,
Hesse-Matrix, Kurven im : partielle Ableitungen,
totale Ableitung (Jacobi-Matrix), Gradient, Mittelwertsätze, Taylor-Entwicklung,
Hesse-Matrix, Kurven im
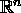 . .
- Satz über implizite Funktionen, lokale Umkehrbarkeit von
Funktionen
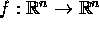 , Extrema mit Nebenbedingungen. , Extrema mit Nebenbedingungen.
- Gewöhnliche Differentialgleichungen: Richtungsfeld, Variablentrennung,
lineare Differentialgleichungen 2. Ordnung, insbesondere Schwingungsdifferentialgleichung.
3. und 4. Semester
- Integralrechnung im
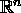 (Lebesgue-Integral), Volumenberechnung, Satz von Fubini, Transformationsformel, Konvergenzsätze.
(Lebesgue-Integral), Volumenberechnung, Satz von Fubini, Transformationsformel, Konvergenzsätze.
- Untermannigfaltigkeiten des
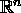 ,
insbesondere Flächen im ,
insbesondere Flächen im
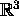 und Berechnung von deren Inhalt, Vektoranalysis, Sätze von Stokes im
und Berechnung von deren Inhalt, Vektoranalysis, Sätze von Stokes im
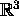 und Gauß im
und Gauß im
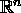 . .
Anmerkungen:
Die angegebene Reihenfolge berücksichtigt nicht nur systematische und
didaktische Gesichtspunkte, sondern auch die bestehenden inhaltlichen Verknüpfungen
mit den parallel laufenden Veranstaltungen über Lineare Algebra und
Analytische Geometrie sowie Numerische
Mathematik. Abweichungen von dieser Reihenfolge sollten deshalb mit den
Veranstaltern dieser Kurse abgestimmt werden.
Nicht alle Punkte müssen rigoros behandelt werden (Beispiel: Fourier-Reihen).
Als Vorlesungstext geeignete Lehrbücher sind u.a.:
- K. Königsberger: Analysis 1,2, Springer;
- O. Forster: Analysis 1, 2, 3, Vieweg;
- K. Endl, W. Luh: Analysis I, II, Akademische Verlagsgesellschaft;
- H. Heuser: Lehrbuch der Analysis 1, 2, Teubner.
Lineare Algebra und Analytische Geometrie
Die Lineare Algebra und Analytische Geometrie ist ein grundlegendes mathematisches
Werkzeug zur Behandlung von Problemen der Geometrie und zur
Lösung von Systemen linearer Gleichungen. Eine zentrale Rolle spielen
lineare Abbildungen und ihre Darstellung durch Matrizen.
1. Semester
- Anschauungsraum (Translationen, Länge und Richtung von Vektoren, Winkel, Geraden
und Ebenen, Parallelität, Vektor- und Spatprodukt).
- Körper, Vektorräume: Linearkombination, Erzeugnis, lineare Abhängigkeit,
Basis, Dimension, Unterräume.
- Skalarprodukt: Orthogonalität, euklidische Norm,
Cauchy-Schwarzsche Ungleichung, Orthogonalisierung
- Lineare Abbildungen und Matrizen: Matrizenkalkül, Darstellungsmatrix, Basiswechsel,
invertierbare Matrizen (allgemeine lineare Gruppe).
- Lineare Gleichungssysteme: Rang einer Matrix, Lösbarkeitskriterien, Struktur der
Lösungsmenge (affine Räume), Gauß-Algorithmus.
2. Semester
- Determinanten, Volumina von Parallelotopen, Orientierung.
- Eigenwerte und -vektoren von Matrizen, charakteristisches Polynom.
- Normalformen von Matrizen: Diagonalisierung, Trigonalisierung, Jordansche Normalform.
- Lineare Abbildungen von Skalarprodukträumen (orthogonale, normale, hermitesche
Matrizen), Beispiele: Drehungen, Spiegelungen (zugehörige Gruppen), Hauptachsentransformation,
Kurven und Flächen zweiter Ordnung.
Anmerk-Algorithmus.
2. Semester
- Determinanten, Volumina von Parallelotopen, Orientierung.
- Eigenwerte und -vektoren von Matrizen, charakteristisches Polynom.
- Normalformen von Matrizen: Diagonalisierung, Trigonalisierung, Jordansche Normalform.
- Lineare Abbildungen von Skalarprodukträumen (orthogonale, normale, hermitesche
Matrizen), Beispiele: Drehungen, Spiegelungen (zugehörige Gruppen), Hauptachsentransformation,
Kurven und Flächen zweiter Ordnung.
Anmerkungen:
Die angegebene Reihenfolge berücksichtigt nicht nur systematische und
didaktische Gesichtspunkte, sondern auch die bestehenden inhaltlichen Verknüpfungen
mit den parallel laufenden Veranstaltungen über Analysis und Numerische
Mathematik. Abweichungen von dieser Reihenfolge sollten deshalb mit den
Veranstaltern dieser Kurse abgestimmt werden.
Nicht alle Punkte müssen rigoros behandelt werden
(Beispiel: Jordansche Normalform).
Durchgehend sollte die Verbindung der Linearen Algebra zur Analytischen
Geometrie deutlich werden (Motivation, Veranschaulichung).
Weitere wünschenswerte Inhalte sind Dualräume und Quotientenräume.
Als Vorlesungstext geeignete Lehrbücher sind u.a.:
- G. Fischer: Lineare Algebra (sowie ergänzend: Analytische Geometrie),
Vieweg;
- B. Artmann: Lineare Algebra, Birkhäuser;
- H.-J. Kowalsky, G. O. Michler: Lineare Algebra, de Gruyter;
- M. Koecher: Lineare Algebra und analytische Geometrie, Springer.
Numerische Mathematik
Die Lehrveranstaltung ,,Numerische Mathematik`` befasst sich mit
grundlegenden numerischen Problemen, die eng an die Inhalte von
,,Analysis I,II`` sowie von ,,Lineare Algebra und Analytische Geometrie I,II``
angelehnt sind.
Gegenstand der Veranstaltung sind numerische Algorithmen, die mit Hilfe
einer höheren Programmiersprache auf einem Computer implementiert werden.
2. Semester
- Zahlendarstellung auf dem Rechner: Gleitpunktdarstellung, Rundungsfehler, Maschinenzahlen,
Maschinengenauigkeit, Auslöschung.
- Polynom- und Splineinterpolation: Interpolationsaufgabe, Lösbarkeit, Darstellung
des Interpolationspolynoms (Lagrange, Newton), Interpolationsfehler, Tschebyscheff-Knoten,
kubische Splines.
- Numerische Integration: Newton-Cotes-Formeln (Trapezregel, Simpsonregel),
zusammengesetzte Formeln, Fehlerabschätzung, Gauß-Formeln und orthogonale Polynome.
- Lineare Gleichungssysteme: Gauß'sches Eliminationsverfahren, LR-Zerlegung,
Cholesky-Zerlegung, Pivotstrategien.
3. Semester
- Lineare Optimierung: Modellaufgaben, Formulierung einer Standardaufgabe,
Basislösungen, Simplexverfahren.
- Ausgleichsprobleme: Polynomausgleich (u.a. lineare Regression) und
überbestimmte lineare Gleichungssysteme, Normalgleichungen,
Orthogonalisierungsmethoden (QR-Zerlegung).
- Nichtlineare Gleichungen und Gleichungssysteme, Iterationsverfahren:
Einführung von Iterationsverfahren über Linearisierung (Newton-Verfahren),
lokale Konvergenz, Kontraktionsprinzipien als theoretisches Mittel zur
Konvergenzanalyse, quadratische Konvergenz, Iterationsverfahren
bei linearen Gleichungssystemen (Gesamtschritt- und Einzelschrittverfahren)
und ihre Konvergenzanalyse über das Spektrum.
- Eigenwertaufgaben:
v. Mises-Verfahren, inverse Iteration, QR-Verfahren in den algorithmischen Ansätzen.
Anmerkungen:
Die Semesterunterteilung (und zum Teil auch die Reihenfolge der Punkte) bezieht sich auf den
zweisemestrigen Kurs für die Diplom-Studiengänge Mathematik und Technomathematik;
für die Studiengänge Wirtschaftsmathematik und Lehramt Oberstufen wird jeweils im
Sommersemester ein einsemestriger Kurs mit im wesentlichen gleichen Inhalten
angeboten.
Grundkenntnisse einer höheren Programmiersprache werden vorausgesetzt (oder ausnahmsweise nach
vorheriger Ankündigung in der Veranstaltung mitbehandelt); für den einsemestrigen Kurs ist der vorherige
Besuch eines Programmierkurses in jedem Fall obligatorisch.
Optional sind noch die folgenden Themen denkbar:
Dualität bei Optimierungsaufgaben,
Bézier-Kurven,
Fast Fourier Transformation (FFT) und trigonometrische Interpolation,
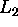 -Approximation von Funktionen und orthogonale Polynome,
Singulärwertzerlegung,
SOR-Verfahren, Verfahren der konjugierten Gradienten. -Approximation von Funktionen und orthogonale Polynome,
Singulärwertzerlegung,
SOR-Verfahren, Verfahren der konjugierten Gradienten.
Als Vorlesungstext geeignete Lehrbücher sind u.a.:
- G. Opfer: Numerische Mathematik für Anfänger, Vieweg;
- J. Werner: Numerische Mathematik 1, 2, Vieweg;
- P. Deuflhard, A. Hohmann: Numerische Mathematik I, de Gruyter.
Mathematische Stochastik
Diese Lehrveranstaltung führt in Denkweisen, Begriffsbildungen und Methoden
der Stochastik ein. Sie ist der Entwicklung und mathematischen
Grundlegung stochastischer Modelle gewidmet. Darüberhinaus werden
statistische Methoden anhand von Beispielen behandelt.
- Der Wahrscheinlichkeitsraum: Allgemeines Modell, Rechenregeln für
Maßräume, diskrete W-Räume und Zufallsvariable, erste Beispiele statistischer
Schlußweise.
- Mehrstufige diskrete Modelle: Koppelung, Produktmodelle, erste Beispiele für
Markov-Ketten, stochastisch unabhängige diskrete Zufallsvariable, elementare bedingte
Wahrscheinlichkeit.
- Grundlegende Modelle diskreter Zufallsexperimente: Bernoulli(p) Verteilung,
Bernoullisches schwaches Gesetz der großen Zahlen, Binomialverteilung, Konfidenzintervall
und Test für p, Satz von de Moivre-Laplace, Poisson Experimente und
Maximum Likelihood Schätzung, Multinomialverteilung, hypergeometrische Verteilung,
geometrische Verteilung, diskrete Erwartungswerte und Streuung.
- Zufallsexperimente über
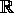 und und
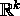 : Borel : Borel
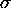 -
Algebra, Verteilungsfunktion, Konstruktion von W-Maßen über -
Algebra, Verteilungsfunktion, Konstruktion von W-Maßen über
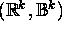 ,
W-Maße mit Riemann-Dichten, Erwartungswert, Streuung, Kovarianz, mehrdimensionale
Normalverteilung, Erzeugung von Zufallszahlen. ,
W-Maße mit Riemann-Dichten, Erwartungswert, Streuung, Kovarianz, mehrdimensionale
Normalverteilung, Erzeugung von Zufallszahlen.
- Koppelung allgemeiner Zufallsexperimente: Messbare Funktionen und Maßintegral,
Erwartungswerte, bedingte Wahrscheinlichkeit, stochastische Unabhängigkeit, Satz von
Fubini, Transformationssatz für Lebesgue-Dichten, schwaches Gesetz der großen
Zahlen, Zentraler Grenzwertsatz.
Anmerkungen:
Als Vorlesungstext geeignete Lehrbücher sind u.a.:
- K. Behnen und G. Neuhaus:Grundkurs Stochastik, Teubner;
- K. Hinderer: Grundbegriffe der Wahrscheinlichkeitstheorie, Springer;
- D. Plachky, L. Baringhaus, N. Schmitz: Stochastik I, D.Plachky: Stochastik
II, Akademische Verlagsgesellschaft.
3.3.2003
|