TALK CANCELLED

What does it mean to "apply" mathematics? How does this "applicability" reflect in the attitudes of practitioners to questions having to do with aesthetic values, ontology, and other foundational matters? We approach this question via several historical case studies from the late 19th to mid-20th century, in an effort to develop a vocabulary for the analytical description of application that reflects the actual range of uses by various flavours of applied mathematicians.

Edmund Husserl analyzed in his The Origin of Geometry (1936) extensively the construction of objectivity of ideal objects, e.g., geometry or mathematics in general (Husserl, 1970).

Based on this work we will argue that the later Husserl can be seen as a precursor of constructivism. In François (2011), I extensively elaborated on the way how Husserl explains the possibility of ideal objectivity, the objectivity of mathematics, and of objectivity of real objects, starting from the really intra subjective process of consciousness. Husserl never struggled with a solipsism nor with the radical constructivism key problem of inter-subjectivism (Martinez-Delgado, 2002). Based on his idealistic transcendentalism and faithful to his basic principles of phenomenology Husserl, or let me call it, the late Husserl analyses the construction of knowledge and more the construction of objective knowledge, e.g., mathematics.

There are many similarities between von Glasersfeld's—the founding father of radical constructivism—concept of radical constructivism and Husserl's phenomenological ideas on the construction of (objective) knowledge. In his famous book Radical constructivism: A way of knowing and learning von Glasersfeld (1995) introduces his concept of radical constructivism in a simple and clear way. "What is radical constructivism? It is an unconventional approach to the problem of knowledge and knowing. It starts from the assumption that knowledge, no matter how it is defined, is in the heads of persons, and that the thinking subject has no alternative but to construct what he or she knows on the basis of his or her own experience. What we make of experience constitutes the only world we consciously live in. It can be sorted into many kinds, such as things, self, others, and so on. But all kinds of experience are essentially subjective, and though I may find reasons to believe that my experience may not be unlike yours, I have no way of knowing that it is the same. The experience and interpretation of language are no exception." (von Glasersfeld 1995: 1)

In this paper we will go into the main critiques on the concept of radical constructivism of von Glasersfeld. Therefore we first will introduce the way Husserl was dealing with the construction of mathematical knowledge and how he was dealing with the ontological question. References.

• François K. (2011) On the notion of a phenomenological constitution of objectivity. In: Tymieniecka A-T. (ed.) Analecta Husserliana, issue Transcendentalism overturned. Springer, Dordrecht: 121-137.
• Husserl E. (1970) The origin of geometry. Appendix VI of the crisis of European sciences and transcendental phenomenology. An introduction to phenomenological philosophy. English translation by David Carr. Northwestern University Press, Evanston, IL: 353-378.
• Martinez-Delgado A. (2002) Radical constructivism: Between realism and solipsism. Science Education 86(6): 840-855.
• von Glasersfeld E. (1995) Radical constructivism: A way of knowing and learning. Falmer Press, London.

In 1990, Jens Høyrup coined the term 'sub-scientific mathematics' as distinct from "scientific mathematics" and identified historical practices in Babylonian and Arabic mathematics as sub-scientific. He points out that such practices are exemplified by recreational mathematics to which he assigns a specific heuristic value in the learning and dissemination of mathematics. Thought his distinction has not been well-received, we believe it can very well be adopted to mathematical cultures in a broader context. In our reassessment of the distinction we provide some formal characteristics of sub-scientific mathematical cultures, examples how such cultures flourished in different societies and time periods and how scholarly and sub-scientific mathematical cultures interact and influence each other.

Slides

TALK WILL BE SHOWN AS VIDEO

Academics interested in mathematical practice have traditionally relied upon introspective accounts of leading mathematicians, philosophical or historical case studies, and interviews with small numbers of practicing mathematicians. More recently some have begun to use experimental techniques. But all these methods rely, to a greater or lesser extent, on what I call the assumption of homogeneity: the idea that there is a great deal of similarity between how different research mathematicians behave in mathematical situations. In this talk I review recent evidence which calls into question this assumption, and argue that there are large (mostly unexplained) differences in how mathematicians evaluate both informal arguments and formal proofs. I will then discuss the implications of this heterogeneity for the validity of typical research methods used by the mathematical practice research community.

The word 'practice' means different things to different scholars. I shall survey some of these meanings and ask whether they have anything to offer the study of mathematical cultures. I shall argue that Pickering's 'mangle of practice' view mangles its own insight, and that human agency retains a privileged place in the study of mathematical cultures and practices.

Slides

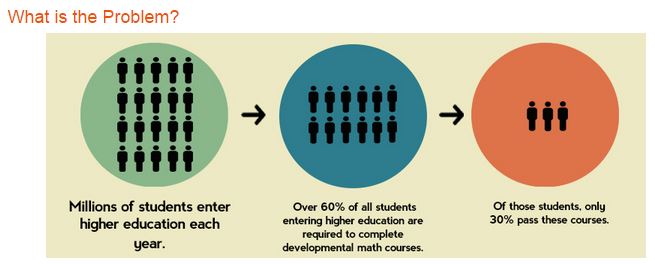
A recent report by the Carnegie Foundation for the Advancement of Teaching (CFAT) begins, "Over 60 percent of all students entering community colleges in the United States are required to complete developmental courses and a staggering 70 percent of these students never complete the required mathematics courses, blocking their way to higher education credentials and with them, a wide array of technical and related careers."

Developmental courses teach pre-college content, such as geometric and basic algebra, and do not count towards degrees as opposed to college algebra a core course representing the "minimum math" required for a college diploma by accreditation standards. If failure to pass college algebra prevents students from completing their degrees one might think the solution is to require more students to take more advanced math in high school. However, more US students are passing more ?advanced? high school mathematics classes than ever before even as they continue to perform poorly on achievement tests. In October 2014 National Public Radio ran a story on CFAT's Pathways project, "Who Needs Algebra? New Approach To College Math Helps More Pass." Reactions varied from, "People use algebra all the time whether they realize it or not" to the less common, "I had to take algebra but have never used it since." A faint refrain from CFAT's target demographic could also be heard, "I tried to get a college degree but couldn't because algebra." From Hobbes's infamous rejection of Wallis's notation, to the Freudenthal-Unguru debate as to whether Euclid Book II is algebra in substance if not style, the borders around algebra continue to defy easy demarcation: Do we need to know what x stands for in order to solve for it? The power symbolic reasoning confers on those who master it is rarely doubted by those who master it! But from the outside looking in, the college algebra requirement appears arbitrary and elitist. This case study suggests that even if mathematics is "universal" insofar as mathematical expertise crosses cultural borders with relative ease, what counts as mathematical competence continues to divide, rather than connect, social classes within contemporary US culture.

Slides

Analysis of online mathematics forums can help reveal how explanation is used by mathematicians. We searched four discussions (Gowers and Tao's Mini-Polymath projects 2009-2012) for premise indicators, conclusion indicators and explanation indicators. We thereby developed typologies of explanations. We found explanations about flaws in reasoning; meta-level reasoning about proof strategies; reasons why the truth of a mathematical statement cannot be known; and clarifications. We investigated the structure of these explanations and the understanding shown by other participants before and after an explanation. Novelties of our approach include an emphasis on mathematics in progress rather than as finished product, a data-led rather than philosophy-led approach, and a focus on the collaborative work characteristic of much mathematical research.

In this talk I will focus on the role of time and memory on one hand and self-reference and some aspects of signification in mathematics on the other hand. Time plays a role at different levels: reading, writing and all other mathematical activities are trivially embedded in time. But what about 'mathematics' itself? My claim is that time cannot be abstracted although some foundationalists and logicians claim that they can base mathematics (or let's say set theory) not on processes (which have to be embedded in time) but on embeddings. I strongly doubt this and will explain why. I am not forgetting about the notion of 'permanence' which seems to resolve the issue but actually does not. The impression of mathematics being something static is due to the phenomenon of memory and 'external memory' like this and other texts is a strange phenomenon, obviously necessary for mathematics. Memory makes it possible to have the illusion of simultaneity - something central to the notion of equality. This leads to another strange role of time in mathematics - many of the metaphors used in mathematics are time-related, related to verbs, like the metaphors we use for limits ... 'n goes to infinity'. This brings us nicely to some semiotic questions. Brian Rotman gives an interesting semiotic model trying to explain what is happening in mathematics - an ideal and abstract 'agent' performs al the operations which are written down (as orders) by a person called 'mathematician'. The issue is that the 'mathematician' does not only write orders (like a computer program) but performs other activities, among others the creation of orders (e.g., programs), the evaluation of orders (programs) created by others. These additional activities are on one hand necessary and lead on the other hand to self-references which themselves constitute strong arguments for the social embedding of mathematics on one hand and for the impossibility to automatize (and formalize) the living part of mathematics and thus mathematics itself. Two examples of self-references would be 'a proof that something is a proof' and 'a rigorous definition of rigor'. Other examples will be presented in the talk.

TALK CANCELLED

In this talk I will examine the introduction of computer graphics to mathematical practice and education starting in the 1970s. I ask how this new technology both complemented and amended older mathematical practices such as hand-drawn illustrations and three-dimensional physical modeling. Focusing on some of the earliest appropriations of computer graphics in geometry and topology—visualizations of higher dimension, the problem of minimal surfaces, and the sphere eversion—I demonstrate how these graphic investigations opened up the numinous mathematical world to direct observation, exploration, and manipulation. I argue that beyond their use in pedagogical work or as aids to theorem proving, these graphic explorations point to the ways in which mathematicians materially explore and generate embodied understandings of otherwise abstract principles.

Philosophers studying mathematical practice typically characterize proofs as the informal conceptual proofs that mathematicians ordinarily produce. I propose that proofs can be characterized by George Lakoff?s notion of cluster concept. I test theoretical entailments of this characterization with an empirical psychological study of mathematicians. I then use the data from this study to investigate the different ways in which different sub-groups of mathematicians view proof.

Slides