Curve Evolution

Strategy

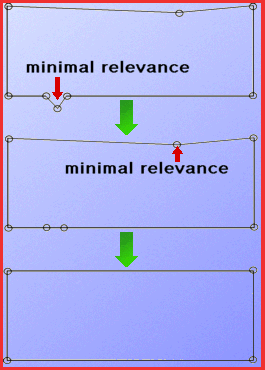
Assigning a relevance measure to every vertex, we can simply take out the least important vertex by direct connection of its neighbours. We repeat this elimination until we obtain the desired stage of abstraction. This simple strategy is shown in the figure on the left.

We define each vertex by its joining line segments and express the relevance measure by a cost function K, giving the cost of eliminating this vertex. The cost function will be derived later.


The algorithm can stated as:
Let Dm=s0,...,sm-1 be a decomposition of a digital curve C into consecutive maximal digital line segments.
The decomposition Dk for each stage of the curve evolution k=m, m-1,..., 3 until Dk-1 is convex is achieved by:

Curve Evolution Procedure (Dm)

  • k=m
  • DO
    • Find in Dk a pair si,si+1 (mod k) such that K(si,si+1) is minimal ;
    • Dk-1= Dk with segments si,si+1 replaced by the line segment s' that joints the endpoints of arc si v si+1 ;
    • k=k+1 ;
  • until Dk-1 is convex.

Remarks:
This algorithm is guaranteed to terminate, since in every evolution step, the number of digital line segments in the curve decomposition decreases by one (one line segment replaces two adjacent segments). It is also obvious that this evolution converges to a convex polygon, since the evolution will reach a state where there are exactly three line segments in the curve decomposition, which clearly form a triangle. Of course, for many curves a convex polygon with more than three sides can be obtained in an earlier stage of the evolution. Thus we obtain:

Curve evolution by digital linearization converges to a convex polygon.

Goon! Continue with Curve Evolution: Relevance Measure