Curve Evolution

The Relevance Measure

As we have seen, the algorithm is very simple, but it can work only if the vertices are eliminated in the right order; hence the relevance measure, which assigns a value of importance to every vertex, plays the key role.
We will first motivate our measure, then derive the formula, at least we will give a geometric and a physical interpretation.

Motivation

It seems that the measure of relevance for a given vertex can be based on two parameters, relative length and turn angle of the adjacent line segments. We assume that the larger the relative length and the turn angle, the greater is its contribution to the shape of a curve. Thus, the cost function K is monotone increasing with respect to the relative length and the total curvature. This assumption can be justified by the rules on salience of a limb in Siddiqi and Kimia [16].

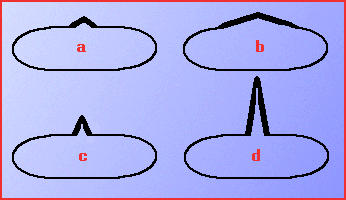
figure1 It can be also motivated by the example objects in the figure on the right:
The bold arc in (b) has the same turn as the bold arc in (a) but is longer, and the bold arc in (c) has the same length as the bold arc in (a) but its turn is greater.

While the bold arc in (a) can be interpreted as an irrelevant shape distortion, the bold arcs in in (b) and (c) are more likely to represent relevant shape properties of the whole object. As it can be easily observed, the contribution of the bold arc in (d) to the shape of the displayed object is the most significant. This arc has the largest turn as well as the largest length.

If you are interested in further details, please send an email to us.

Goon! Continue with Curve Evolution: Properties