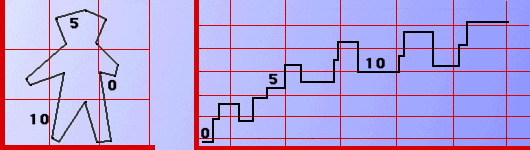
 For example, this figure shows
a digital curve and its step function representation in the tangent space.
For example, this figure shows
a digital curve and its step function representation in the tangent space.
 Introduction
IntroductionFor all coming steps we will not use the polygonal representation of the shape, but we will transform it into tangent space.
A digital curve C is represented in the tangent space by the graph of a step function, where the x-axis represents the arclength coordinates of points in C and the y-axis represents the direction of the line segments in the decomposition of C.
We will call each horizontal line segment in the graph of the step function a step. We traverse a digital curve in the counter clockwise direction and assign to each maximal line segment in the curve decomposition a step in the tangent space. The y-value of a step is the directional angle of the line segment and the x-extend of the step is equal to the length of the line segment normalized with respect to the length of the curve.
 For example, this figure shows
a digital curve and its step function representation in the tangent space.
For example, this figure shows
a digital curve and its step function representation in the tangent space.
If your browser supports JAVA-APPLETS, you can click
 here
to paint your own shape and see its tangent space representation.
here
to paint your own shape and see its tangent space representation.
Formally, the tangent space is a torus S1 x S2, where S1 is a circle of length one that represent the length of a digital curve and S2 is a circle that represents the angular direction of digital line segments.
We will display the tangent space as a rectangle with
the parallel sides identified in the standard way
to obtain a topological torus.
The y-difference between two adjacent steps in the tangent space represents
the turn angle of the corresponding pair of line segments.
As we will introduce the relevance measure for our curve evolution, we
will see that the significance of the contribution of a pair of consecutive line segments
to the shape depends on their length and the turn angle in the direction
of traverse.
Exactly these two parameters are represented in the tangent space.
Formal Description
We assume that the digital plane Z2 is embedded in the plane
R2 in the standard way, i.e., as a grid of points with integer coordinates.
Let C: {p0, ..., pn } -> Z2 be a digital 8-curve with
C(p0) = C(pn)
parameterized by the normalized arclength, which
can be achieved by the following construction:
Let arclength(C(pk)) denote the distance of point C(pk) from point C(p0) measured (in R2) while traversing C in the counter clockwise direction. We normalize the length of curve C so that its total length is one, i.e., arclength(C(pn)) = 1. A digital curve C is traversed in the counter clockwise direction and divided into maximal digital line segments s1, ..., sm (see Chapter First Steps). For a line segment s in C , we define length(s) to be the length of s normalized by the length of C,
length(s) = arclength(end(s)) - arclength(beginning(s))
where end(s) is the endpoint of s and beginning(s) the beginning point of s. We also define angle(s) to be the angular direction of line segment s in the standard coordinate system of the plane.Now we define a transformation T mapping a digital 8-curve to the tangent space. For illustrations, see Figures \ref{symmetry}(a) and (b). To each digital line segment s of { s1, ..., sm }, a line segment T(s) in the tangent space is assigned such that
py(T(s)) = angle(s)
andpx(T(beginning(s))) = arclength(beginning(s)) , px(T(end(s))) = arclength(end(s))
where px and py denote the projections on x- and y-axes in the tangent space, correspondingly.
This means that
y-value of all points in T(s) is equal to angle(s)
and the projection of T(s) on the x-axis has
the same (normalized) arclength coordinates as s in C.
This implies that the length
of T(s) is equal to length(s).
References
An analytical description of the transformation
to the tangent space for continuous curves
can be found in Zahn and Roskies, see [22].
They call the step function in the tangent space
a cumulative angular bend function.
Zahn and Roskies use this transformation only as an
intermediate step to obtain Fourier descriptions
of planar curves.
They neither use the tangent space for analyzing the underlying
planar curves nor for scale transformations,
which we will describe below.
Uesaka [21] uses the transformation of polygonal arcs to the tangent space to determine a circular approximation of polygonal arcs.
 Continue with Curve Evolution
Continue with Curve Evolution