 If you are not interested in details, you can
skip the formal description and continue with results.
If you are not interested in details, you can
skip the formal description and continue with results.

 If you are not interested in details, you can
skip the formal description and continue with results.
If you are not interested in details, you can
skip the formal description and continue with results.
Definitions:
We denote:

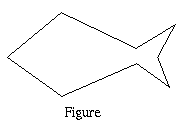 curve C=(s0,...,sns): the polygonal digital curve, representing the shape, consisting of
(ns+1) line segments.
curve C=(s0,...,sns): the polygonal digital curve, representing the shape, consisting of
(ns+1) line segments.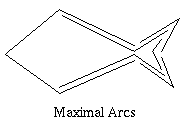 We decompose the curve C into maximal convex/concave arcs ma:
We decompose the curve C into maximal convex/concave arcs ma:
 We derived a measure for arc comparison, for details click here.
We derived a measure for arc comparison, for details click here.
It is not possible, to make a simple one to one comparison of maximal convex/concave arcs ma, due to the following reasons:
Definition:
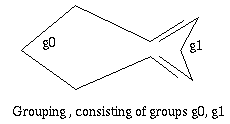 A group g is a polygonal subarc of the curve C, consisting of the segments
of consecutive maximal arcs:
A group g is a polygonal subarc of the curve C, consisting of the segments
of consecutive maximal arcs:
g:=(sstart,...,send), start>=0, end<=ns,
where
Definition:
A grouping G is an ordered set of consecutive groups, covering the whole
curve C:
G:=(g0,...,gng)
where
Given two curves C1,C2 their comparison can be defined as a mapping on a special subset of groupings SG1,SG2, called the correspondence:
Definition:
We call a relation CO on SG1 x SG2
a correspondence if:
At least, the comparison between the curves:
Definition:
Given two curves C1,C2, we define a mapping GM
on the correspondence CO, called the groupmatching:
GM:
 For a description of the arc-comparison click here.
For a description of the arc-comparison click here.
With these definitions, we can easily formulate the task for comparison:
Find the element BE in the correspondence CO such that the groupmatching is minimal, i.e. GM(BE)<=GM(e) for all elements e in CO.
Note that the grouping takes respect of the order of groups, and hence of the order of
the digital segments. This means, that in every element (G1,G2)
in CO the first groups g0(G1) and g0(G2)
always contain the first digital segment of their corresponding curves.
This leads to the problem, that for an intuitive groupmatching the correct starting point
must be found. We will come later to the solution of this problem.
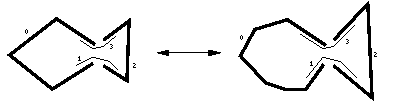 We will explain the strategy by a special example, see curve right. The two fishlike
shapes are decomposed into three maximal arcs each. We want to find the minimal correspondence
(intuitively we expect that the best correspondence is a one to one mapping of each maximal arc).
We will explain the strategy by a special example, see curve right. The two fishlike
shapes are decomposed into three maximal arcs each. We want to find the minimal correspondence
(intuitively we expect that the best correspondence is a one to one mapping of each maximal arc).
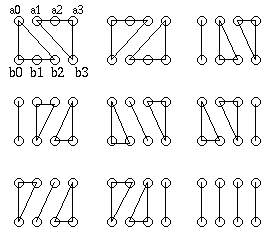 The figure on the left
shows the correspondence CO between the left fish (a), which is composed of
the arcs a0 to a3, and the right one (arcs
a0 to a3).
The figure on the left
shows the correspondence CO between the left fish (a), which is composed of
the arcs a0 to a3, and the right one (arcs
a0 to a3).
CO consists of all possible combinations of groupings that hold the conditions stated in its definition above.
We assign a value to each of the nine elements of CO by the groupmatching.
Finding the best comparison be explained by the following graph:
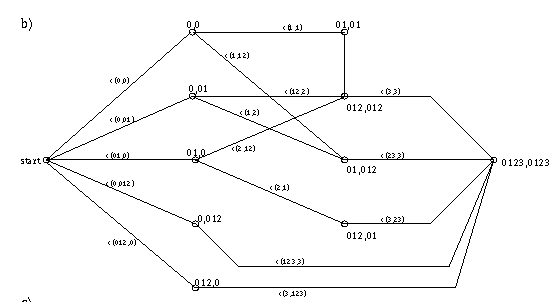
Hence to get the best comparison is the task to find the cheapest way in the graph.
This is typically solved by dynamical programming.
 Continue with Results
Continue with Results