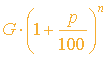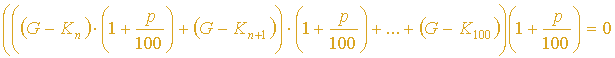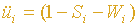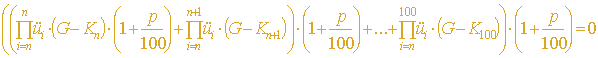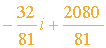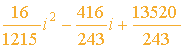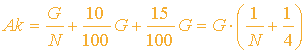LÖSUNG / ERGEBNIS

Herleitung der Formel

Jeder Versicherte zahlt einen festen monatlichen Betrag, den wir für unsere weitere Rechnung auf einen Jahresbeitrag hochrechnen. Der Betrag wird jährlich verzinst. D.h. wir führen unsere weitere Berechnung auf die Zinseszinsrechnung zurück. Ziel ist es vorerst einen Betrag G auszurechnen, der die durchschnittlichen Kopfschäden, d.h. Kosten eines Versicherten deckt.

Es gilt:

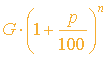
G ist dabei der Grundbetrag und p der Zinssatz, zu dem der Betrag angelegt wird. Wir gehen bei unseren Rechnungen von einem Zinssatz von 3,5 % aus. Es gilt aber noch zu bedenken, daß nicht die gesamten Beträge angelegt werden können, da die Versicherten bedauerlicherweise auch Schaden verursachen. Der muß angerechnet werden. Den durchschnittlichen Pro-Kopfschäden in Abhängigkeit des Lebensalters und des Geschlechtes sind aus offiziellen Statistiken abzulesen. Diese Beträge sind von dem zu verzinsenen Betrag im entsprechenden Jahr abzuziehen. Das verkompliziert die Formel wie folgt.

Es gilt:

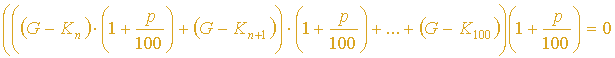
K_n ist dabei der durchschnittliche Kopfschaden im Jahr n. Die allgemeine Zinseszinsformel (siehe oben) gilt nicht mehr, da der Zinsbetrag von Jahr zu Jahr variiert und nicht stetig bleibt (wegen der unterschiedlichen Kopfschäden). Mit dem Älterwerden von Menschen steigen auch deren Kosten, d.h. es kann vorkommen, daß der Zinsbetrag für ein spezifisches Jahr negativ wird. Daraus folgt, dieser Term verursacht Kosten, der von dem bisherigen Betrag abgezogen wird (negatives Vorzeichen in der Zinssumme). Das Konzept ist, in den Anfangsjahren eines Menschenlebens, wo er statistisch weniger Schäden verursacht einen gewissen Betrag anzuhäufen, von dem man die späteren Kosten des Versicherten deckt. (Das ist der Grund, weshalb ein späteres Eintreten in eine Versicherung teurer ist). In unserer Rechnung wollen wir zunächst keinen Gewinn erwirtschaften, setzen die Formel also gleich null. Außerdem ist zu bedenken, daß Versicherte zur Konkurrenz wechseln, kündigen oder die körperliche Welt verlassen. Dafür erstellen wir einen Faktor Ü. Der beinhaltet Sterbewahrscheinlichkeit und Stornowahrscheinlichkeit.

Es gilt:

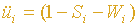
Ü_i gibt die wahrscheinliche Verweildauer eines Versicherten in der Versicherung für das Jahr i an (Ü wie Überlebt). Für die prozentualfaktorielle Umrechnung werden die Sterbewahrscheinlichkeit in Abhängigkeit des Alters (S_i) und die Stornowahrscheinlichkeit in Abhängigkeit des Alters (W_i) auf Dezimalzahlen gebracht. Die Berechnung von Un erfolgt später, Sn ist erneut aus offiziellen Statistiken abzulesen. Üi wird ebenfalls in die Formel einbezogen und zwar als Durchschnittsfaktor der Wahrscheinlichkeiten. Ün muß ebenfalls aufmultipliziert werden, denn die Wahrscheinlichkeit 24 Jahre alt zu sein und dann 25 Jahre alt zu werden mag zwar genauso groß sein, wie danach sogar 26 zu werden, doch die Wahrscheinlichkeit 24 zu sein und später einmal 26 zu werden, ist geringer.

Es gilt als endgültige Formel zur Errechnung des Grundbetrages:

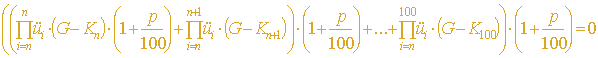
Zurück nach Oben

Berechnung der Stornowahrscheinlichkeit

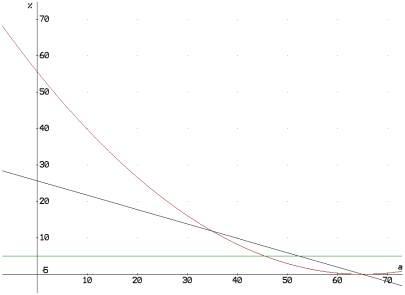
Die Stornowahrscheinlichkeiten (W_i) müssen ebenfalls in diese Rechnung einfließen und dafür gibt es keine statistischen Erhebungen, denn Menschen sind seltsame Wesen. Wir quantifizieren nun die Austrittswahrscheinlichkeit auf 5%, was etwa realistisch ist. Jedoch macht es Unterschiede, ob konstant fünf Prozent der Versicherten austreten oder ob anfangs mehr und später weniger Versicherte austreten (und im Schnitt wieder 5%). Wir haben drei Stornomodelle kreiert. Das konstante, das lineare und das parabolische (siehe Grafik). Das konstante Modell ist trivial, für das lineare ergibt sich eine Funktion. Von der Funktion sind der einbeschriebene Flächeninhalt und der Schnittpunkte mit der X-Achse bekannt. Denn der Flächeninhalt ergibt sich aus dem konstanten Modell (schließlich soll das lineare Modell den quantitativen Austrittsanteil genauso erfassen, wie das unrealistische konstante Modell). Den Schnittpunkt mit der X-Achse, d.h. die Austrittswahrscheinlichkeit von 0%, haben wir auf 65 Jahre festgelegt. Denn Oma Frida mit der Riester-Rente wird einen Versicherungswechsel in diesem betagten Alter weder geistig noch finanziell verkraften. Außerdem legen wir ein Eintrittsalter von 20 Jahren fest, weil vorher ein Eintritt in eine private Versicherung eher unrealistisch ist (Elternentscheid, Mitversicherungen etc.).
Für die lineare Abnahme der Austrittswahrscheinlichkeiten für das Jahr i ergibt sich nach trivialer Rechnung:

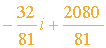
Die parabolische Beschreibung der Austrittswahrscheinlichkeiten halten wir aber für realistischer, da in den Anfangsjahren die Lebensumstände der jungen Wilden unsicherer sind, als im Alter. Und wir sind der Meinung dieses Phänomen nimmt nicht konstant ab. Allgemein gilt: ax² + bx + c Für die Koeffizienten a,b,c brauchen wir drei Bezugspunkte zum Ausrechnen. Der eine ist wieder der Schnittpunkt mit der X-Achse bei 65 Jahren (Scheitelpunkt der Funktion). Der Zweite Bezugspunkt ergibt sich aus der Ableitung der Funktion an der Stelle X = 65 Jahre. Denn dort muß die erste Ableitung Null sein. Der dritte Bezugspunkt läßt sich aus dem Integral der Funktion erschließen, da auch die durchschnittliche Austrittswahrscheinlichkeit wieder 5% sein soll. Nach trivialer Rechnung ergibt sich:

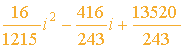
Nun die drei Modelle im Vergleich:

D.h. unsere dicke Formel vom Anfang ist mit der Formel für Ü_i jetzt fast komplett. Wir können jetzt einen Betrag ohne Reingewinn ausrechnen (mittels entsprechendem Programm und viel Tipparbeit). In dem beistehenden Programm gehen wir von einer Lebensdauer von 100 Jahren aus.

Zurück nach Oben

Berechnung der Abschlußkosten

Nun kommen wir zu dem für die Versicherung wichtigen Teil. Knete machen. Vorerst muß die Versicherung erst einmal an den Mann gebracht werden, die Bearbeitungskosten kommen hinzu (Angestellte, Miete für Räumlichkeiten und natürlich der gesetzlich festgeschriebene Sicherheitszuschlag von 15%. Diese weitere Kostenbelastung nennen wir Abschlußkosten. Hier sei noch einmal betont, daß bisher nur Kosten gedeckt, bzw. gesetzliche Auflagen erfüllt, und kein Gewinn erwirtschaftet wird.

Es gilt:

Ak = T + B + S

Die Tantieme T ist derjenige Teil, den der Versicherungsagent für die Vermittlung kassiert. Im allgemeinen ist dies 3*G, wobei die Versicherung dies natürlich auf die wahrscheinlich versicherten Jahre des Versicherten mittelt und aufschlägt, also 3*G/N. Der Sicherheitszuschlag S wird mit 15/100 G veranschlagt und die Bearbeitungsgebühr pauschalisieren wir jetzt einfach auf 10%, also 1/10 G.

Es folgt:

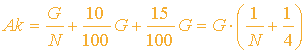
N gibt die Anzahl der Jahre an, die man wahrscheinlich versichert ist. Berechnung erfolgt wieder mittels Statistiken von Sterbe- und Stornowahrscheinlichkeiten.

Zurück nach Oben

Interpretation des Ergebnisses

Zur Verdeutlichung wird die Applikation unserer Software herangezogen, die zu folgendem Ergebnis führt: Die Person in unserem Beispiel ist 25 Jahre alt und weiblich. Gemäß unserem die oben genannte Formel verwendendem Programm müßte sie 6800,37 DM im Jahr zahlen. Eine reale Person, erfüllt auch diese Bedingungen und zahlt 14400 DM pro Jahr. Unsere Formel zielt jedoch nur auf eine Kostendeckung ohne Gewin ab, während die Versicherungen natürlich Profit erwirtschaften wollen. Weiterhin haben wir einige negative Aspekte nicht beachtet, wie z.B. die steigenden Medikamentenkosten, die Einschränkungen durch den Gesetzgeber, die sich ändernde Altersstruktur oder die ständige Neuerungen von Gesetzen. Doch auch nach Berücksichtigung dieser Faktoren läßt sich die große Abweichung nur erklären, wenn der Betrag nicht konstant gelieben ist.

Wir können nicht richtig, wir können nur billig. :-)

Zurück nach Oben