Lorenz Gleichungen
Seminar Dynamische Systeme
SS 2006
Aleksander Hinz
Fragestellung
Probe mit einem Computer das Wetter auf nichtlinearem und nicht statistischem Weg zu beschreiben.
Betrachtet wird zunächst eine 2 dimensionale Schicht (Flüssigkeit / Gas) welche von unten angeheizt wird. Dies entspricht der Erdaufheizung der Erde durch die Sonne und der Atmosphere. Es herrsche die Temperaturdifferenz von 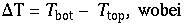
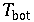
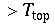 .
.
Ist diese klein so gibt es keine Bewegung und die Temperatur wird über die Mohlekühlbewegung allein übertragen (lineares Temperaturverlauf).
Beim weiterem Ausheizen sind Rollen zu sehen
Saltzmann beschrieb diese Bewegung durch:
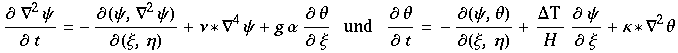
wobei ξ, η räumliche Koordinaten, t die Zeit sind. 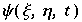 ist die Stromfunktion,
ist die Stromfunktion, 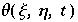 stellt die Temperatur dar, H ist die Höhe der Schicht, g ist die Gravitationskonstante, α ist thermischer Expansionskoeffizient, ν die Viscosität und κ die Thermale Konduktivität.
stellt die Temperatur dar, H ist die Höhe der Schicht, g ist die Gravitationskonstante, α ist thermischer Expansionskoeffizient, ν die Viscosität und κ die Thermale Konduktivität.
Gilt
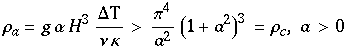
so erhält man die Lösungen
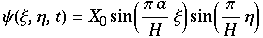
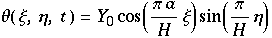
die die Rollen beschreiben ( sind Konstanten). Dies sind stationäre Lösungen, da t keine Rolle mehr spielt.
sind Konstanten). Dies sind stationäre Lösungen, da t keine Rolle mehr spielt.
Mit dem Ziel der besseren Beschreibung für größere ΔT hat Saltzman nun eine Zeitabhängige Fourierentwicklung durchgeführt und die nun zeitabhängigen Koeffizienten als neue Unbekannte gesetzt. 7 physikalisch interessante Gleichungen wurden weiteruntersucht, von denen 3 bei langen Zeiten nicht Null werden.
Lorentz begann Modelierung der zeitlichen Lösungen gleich mit Hinblick auf diese und erhielt:
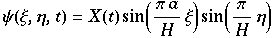
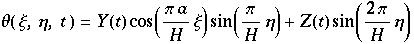
setzt man dies in die Bewegungsgleichungen von Saltzman ein, so erhält man
![Overscript[x, .] = σ (y - x)](HTMLFiles/Lorenz_13.gif)
![Overscript[y, .] = ρ x - y - x z](HTMLFiles/Lorenz_14.gif)
![Overscript[z, .] = - β z + x y](HTMLFiles/Lorenz_15.gif)
wobei
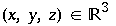 und
und 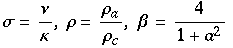
aus physikalischen Gründen wird 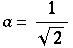 gewählt und somit wird β =
gewählt und somit wird β = 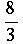 ,
, 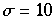 ist typisch für Flüssigkeiten,
ist typisch für Flüssigkeiten, 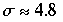 für Wasser,
für Wasser, 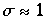 .
.
Lorenz merkte, daß bei seinen Anfangswerten und Anfangsparametern schon kleine Differenzen zu komplett verschiedenen Resultaten führten ⇒ langfristige Wettervorhersage ist unmöglich, da Anfangsdaten immer mit einem gewissen Fehler vorliegen.
Parameterbetrachtungen und Attraktor
Es werden σ und β fixiert und das System unter unter verschiedenen ρ betrachtet
Es gibt eine einfach zusammenhängedne Region 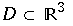 die den Ursprung enthält, sodaß das Vektorfeld nach innen zeigt. Dieses beinhaltet einen Attraktor (Menge)
die den Ursprung enthält, sodaß das Vektorfeld nach innen zeigt. Dieses beinhaltet einen Attraktor (Menge)
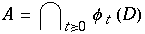
"An attractor is a bounded refion in phase-space, invariant under time evolution, such that the forward trajectories of most, or even all, nearby points converge to it." Strange, wenn "trajectories converging to the attractor are sensitive with respect to the initial conditions"
Lorenzattraktor ist weder hyperbolisch noch strukturell stabil, aber trotzdem "robustes" Verhalten auf (weiter Parameterbereich liefert vergleichbares Ergebniss).
Dieser hat hier das Volumen 0, da die Spur der Jacobideterminante (Divergenz des Vektorfeldes) negativ ist
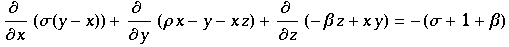
ρ < 1
In[2]:=
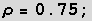
In[17]:=
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... 1] 0.1, z[1] 0.1, x[1] 0.1}, {x, y, z}, {t, 1, 10}, MaxSteps->100000] ;](HTMLFiles/Lorenz_27.gif)
In[18]:=
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 10, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_28.gif)
![[Graphics:HTMLFiles/Lorenz_29.gif]](HTMLFiles/Lorenz_29.gif)
Out[18]=
In[19]:=
![Plot[Evaluate[ x[t] /. %%], {t, 1, 10}]](HTMLFiles/Lorenz_31.gif)
![[Graphics:HTMLFiles/Lorenz_32.gif]](HTMLFiles/Lorenz_32.gif)
Out[19]=
In[20]:=
![Plot[Evaluate[ y[t] /. %%%], {t, 1, 10}]](HTMLFiles/Lorenz_34.gif)
![[Graphics:HTMLFiles/Lorenz_35.gif]](HTMLFiles/Lorenz_35.gif)
Out[20]=
In[21]:=
![Plot[Evaluate[ z[t] /. %%%%], {t, 1, 10}]](HTMLFiles/Lorenz_37.gif)
![[Graphics:HTMLFiles/Lorenz_38.gif]](HTMLFiles/Lorenz_38.gif)
Out[21]=
Allgemein gilt, daß in diesem Fall der Ursprung ein hyperbolischer Tiefpunkt und einizger Attraktor ist
ρ = 1
Hier erhält man die Eigenwerte 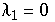 ,
, 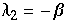 ,
, 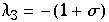 und man erhält eine Heugabel bei einer Wahl von
und man erhält eine Heugabel bei einer Wahl von 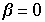
ρ > 1
Der Ursprung ist ein Sattelpunkt mit einer instabilen Untermannigfaltigkeit
Man erhält die beiden nichttrivialen Fixpunkte bei
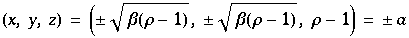
Diese werden zu Tiefpunkten, falls 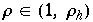 mit
mit 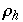 =
= 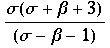
In[55]:=
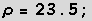
In[60]:=
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... 1] 0.1, z[1] 0.1, x[1] 0.1}, {x, y, z}, {t, 1, 50}, MaxSteps->100000] ;](HTMLFiles/Lorenz_49.gif)
In[61]:=
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 50, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_50.gif)
![[Graphics:HTMLFiles/Lorenz_51.gif]](HTMLFiles/Lorenz_51.gif)
Out[61]=
In[62]:=
![Plot[Evaluate[ x[t] /. %%], {t, 1, 50}]](HTMLFiles/Lorenz_53.gif)
![[Graphics:HTMLFiles/Lorenz_54.gif]](HTMLFiles/Lorenz_54.gif)
Out[62]=
In[67]:=
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... 2513; -0.1, z[1] -0.1, x[1] -0.1}, {x, y, z}, {t, 1, 50}, MaxSteps->100000] ;](HTMLFiles/Lorenz_56.gif)
In[68]:=
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 50, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_57.gif)
![[Graphics:HTMLFiles/Lorenz_58.gif]](HTMLFiles/Lorenz_58.gif)
Out[68]=
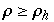
Eine Hopfgabelung tritt bei den beiden Fxpunkten auf (für 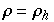 ) und für
) und für 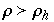 sind alle Fixpunkte instabil, jedoch existiert immer noch eine anziehende Menge
sind alle Fixpunkte instabil, jedoch existiert immer noch eine anziehende Menge 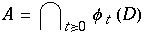
In[3]:=
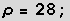
In[8]:=
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... ] 0.1, z[1] 0.1, x[1] 0.1}, {x, y, z}, {t, 1, 100}, MaxSteps->100000] ;](HTMLFiles/Lorenz_65.gif)
In[9]:=
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 100, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_66.gif)
![[Graphics:HTMLFiles/Lorenz_67.gif]](HTMLFiles/Lorenz_67.gif)
Out[9]=
In[10]:=
![Plot[Evaluate[ x[t] /. %%], {t, 1, 50}]](HTMLFiles/Lorenz_69.gif)
![[Graphics:HTMLFiles/Lorenz_70.gif]](HTMLFiles/Lorenz_70.gif)
Out[10]=
In[11]:=
![Plot[Evaluate[ y[t] /. %%%], {t, 1, 50}]](HTMLFiles/Lorenz_72.gif)
![[Graphics:HTMLFiles/Lorenz_73.gif]](HTMLFiles/Lorenz_73.gif)
Out[11]=
In[13]:=
![Plot[Evaluate[ z[t] /. %%%%%], {t, 1, 50}]](HTMLFiles/Lorenz_75.gif)
![[Graphics:HTMLFiles/Lorenz_76.gif]](HTMLFiles/Lorenz_76.gif)
Out[13]=
Semifluß
Betrachtet wird nun ein Semifluß als Grenzwertbetrachtung für den ursprünglichen Fluß für große Zeiten. Dieser hat die Eigenschaften, daß Betrachtungen in zeitlich umgekehrter Richtung das Verzweigungsintervall ![[-a, a]](HTMLFiles/Lorenz_78.gif) erreichen und dort nicht mehr eindeutig feststellbar ist aus welchem Zweig der Fluß kam.
erreichen und dort nicht mehr eindeutig feststellbar ist aus welchem Zweig der Fluß kam.
Die Eindeutigkeit der Lösung von dem Anfangswertproblem ist somit verletzt.
Lorenz benutzte diese Tatsache um Argumentieren, daß A unendlich viele Blätter hat und das Lösungen sich nicht schneiden, sondern von Blatt zu Blatt sich bewegen.
First return map
Betrachtung der Fläche 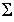 mit der Eigenschaft, daß
mit der Eigenschaft, daß 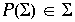 , wobei P eine invertierbare Poincaréabblidung ist.
, wobei P eine invertierbare Poincaréabblidung ist.
Einschränkung von Σ auf das Intervall ![[-a, a]](HTMLFiles/Lorenz_81.gif) und der zu P äquvalenten Abbildung f mit
und der zu P äquvalenten Abbildung f mit
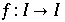
Also ist 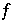 die Poincaréabbildung vom Semifluß
die Poincaréabbildung vom Semifluß
Zeit für den first return ist unterschiedlich und geht gegen ∞ falls man sich der Mitte von 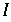 nähert.
nähert.
Über 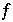 ist folgendes bekannt:
ist folgendes bekannt:
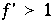 , was deutlich in der sich steigernden Oszillation zu sehen ist
, was deutlich in der sich steigernden Oszillation zu sehen ist
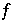 hat keine Fixpunkte in
hat keine Fixpunkte in 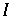
Discontinuität bei y = 0 (gut zu sehen bei 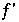 ) , zeigt den Vorzeichenwechsel an
) , zeigt den Vorzeichenwechsel an
weiter gilt:
![f(0^-) = -f(0^+) = a , f(a) = -f(-a) ≻0 , Underscript[ lim, x0] (f ' (x)) = ∞ , f^2(-a) ≻f(a) , f^2(a) < f(-a)](HTMLFiles/Lorenz_90.gif)
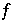 heißt Lorenzabbildung
heißt Lorenzabbildung
Eine Betrachtung beschränkt nur auf 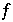 geht sicherlich mit einem Detailverlust einher, genügt aber in erster Näherung.
geht sicherlich mit einem Detailverlust einher, genügt aber in erster Näherung.
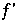 erhält man über:
erhält man über:
![(f^k(p)) ' = Underoverscript[∏, j = 0, arg3] f ' (f^j(p))](HTMLFiles/Lorenz_94.gif)
Dies ist größer als 1, da ale Faktoren selbst bereits größer als 1 sind.
Orbits (unstabile) mit Persiode 2 und 3 sind zu finden über:
Sei ![I_1 =[-a, 0]](HTMLFiles/Lorenz_95.gif) und
und ![I_2 = [0, a]](HTMLFiles/Lorenz_96.gif) , so ist
, so ist
![f(I_1) =[f(-a), a] ⊃ I_2](HTMLFiles/Lorenz_97.gif) und
und ![f(I_2) =[-a, f(a)] ⊃ I_1](HTMLFiles/Lorenz_98.gif) , so daß
, so daß
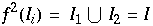 für
für 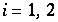
entsprechendes bei
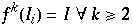
womit
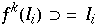
und 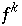 hat somit mindestens 2 Fixpunkte für alle k, woraus folgt, daß
hat somit mindestens 2 Fixpunkte für alle k, woraus folgt, daß 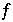 periodische Orbits hat.
periodische Orbits hat.
Weiter gilt (da immer 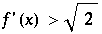 ) : Jedes Subintervall
) : Jedes Subintervall 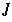 überdeckt nach n Schritten
überdeckt nach n Schritten 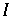 , womit alle Punkte nicht wandernd sind.
, womit alle Punkte nicht wandernd sind.
Weiter gilt: Bereits mit 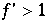 gilt für 2 beliebig nahe Punkte
gilt für 2 beliebig nahe Punkte 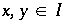 , daß sie Bilder
, daß sie Bilder 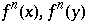 haben, welche auf verschiedenen Seiten von 0 liegen. Ist dies der Fall, so verhalten sie sich völlig unabhängig voneinander und die Orbits sind nicht dicht. Dieses Ausspitten hängt von den Positionen der Urbilder vom Ursprung 0,
haben, welche auf verschiedenen Seiten von 0 liegen. Ist dies der Fall, so verhalten sie sich völlig unabhängig voneinander und die Orbits sind nicht dicht. Dieses Ausspitten hängt von den Positionen der Urbilder vom Ursprung 0, 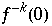 ab. Da
ab. Da 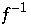 die möglichen Werte verdoppelt, wächst die Anzahl an Urbildern
die möglichen Werte verdoppelt, wächst die Anzahl an Urbildern 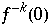 mit
mit 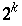 . Nur diese liegen dicht in
. Nur diese liegen dicht in 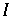 .
.
Die lokale Expansion und das obrige unabhängie Verhalten (deutlich zu sehen an den Urbildern) belibig naher Orbits nennt man sensitive dependence on initial conditions
Der Attraktor und seine Untersuchung
Aus der Tatsache, daß zwei nahe liegende Punkte irgendwann auf verschiedenen Blättern liegen und das es Orbits gibt die dicht liegen, folgt, daß der Attraktor "dynamically indecomposable" ist, d.h. er kann nicht mehr weiter in kleinere geschlossene Stücke geteilt werden, die invariant unter dem Fluß sind.
Allg. läßt sich zeigen, daß jeder Fluß, der die Anfangsgleichungen erfüllt zu einem strange Attrakor tendiern muß.
Weiter läßt sich zeigen, daß robuste Attraktoren einen Sattelpunkt haben müssen und das alle Attraktoren dann die selben Eigenschaften haben wie der hier untersuchte.
Probleme bei der Untersuchung ergeben sich vorallem bei dem Sattelpunkt, da hier die Orbits langsam verlaufen (viele Rechenschritte nötig ⇒ viele numerische Ungenauheiten)
Bild "suspended horseshoe"
Beim Vorhandensein solcher Ebenen kann man schließen, daß es eine endliche Menge an periodischen Trajektorien gibt.
Beweisidee des Attraktors
Beweis geht über zwei Schritte
Zunächst wurde eine Ebene Σ gefunden mit der Region N in Σ. so daß alle Orbits die in n starten auch immer dort zurückfinden / Abdeckung dieser Region N mit Rechtecken / Rechtecke kehren zu Σ zurück.
Problem jedoch wieder der Sattelpunkt !
Welchsel in ein solches Koordinatensystem, sodaß Trajektorein linear angenähert werden können, was besser ist als die integrale numerische Berechung jeden einzelnen Schrittes.
Urbilder und Heimnumerik 
Nun wird f durch die folgende Funktion angenähert:
![f(x) = α 1 - β | x | ; &n ... ; x∈ (0, 1]](HTMLFiles/Lorenz_117.gif)
durch die Wahl von
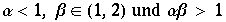
wird
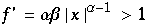
und mit
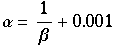
wird die Ableitung nahe bei eins nahe an den Fixpunkten sein. Dies simuliert den langsamen Oszillationsanstieg dort.
In[64]:=
![Show[Plot[-1 + β * (Abs[x])^α, {x, 0, 1}], Plot[1 - β * (Abs[x])^α, {x, -1, 0}], Plot[x, {x, -1, 1}]]](HTMLFiles/Lorenz_121.gif)
![[Graphics:HTMLFiles/Lorenz_122.gif]](HTMLFiles/Lorenz_122.gif)
Out[64]=
Bevor man sich tiefe Rekursionen zu verdeutlichung der Anfangssensibilität anschaut, muß man sich vergewissern wie genau numerisch das benutzte Programm rechnet. Hierzu zunächst die genaue Rechung (d.h.z.B.: Zahlen werden als Brüche behandelt und nicht Näherungsweise als Dezimalzahlen). Man nähme die Anfangswerte
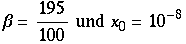
Man erhält für die ersten 45 Iterationen (returns):
![[Graphics:HTMLFiles/Lorenz_125.gif]](HTMLFiles/Lorenz_125.gif)
Führt man nun die selbe Rechnung mit der Standartnäherung durch, so erhält man:
![[Graphics:HTMLFiles/Lorenz_126.gif]](HTMLFiles/Lorenz_126.gif)
Bei 45 Schritten erhält man mit Mathematia eine Abweichung von 0,538611.
Somit ist eine Beschränkung auf 45 Schritte bei dieser Betrachtung sinnvoll.
Zunächst sei
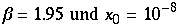
![[Graphics:HTMLFiles/Lorenz_128.gif]](HTMLFiles/Lorenz_128.gif)
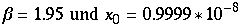
![[Graphics:HTMLFiles/Lorenz_130.gif]](HTMLFiles/Lorenz_130.gif)
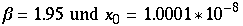
![[Graphics:HTMLFiles/Lorenz_132.gif]](HTMLFiles/Lorenz_132.gif)
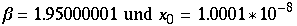
![[Graphics:HTMLFiles/Lorenz_134.gif]](HTMLFiles/Lorenz_134.gif)
Somit kommt man zum Schluß, das nicht nur Lorenzabbildungen sich chaotisch verhalten, sondern auch einparametrige Familien von solchen Abbildungen (womit dies also "vererbt" wird). Auch wird deutlich, das die Urbilder dicht liegen müssen.
(April 17, 2006)
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... 1] 0.1, z[1] 0.1, x[1] 0.1}, {x, y, z}, {t, 1, 10}, MaxSteps->100000] ;](HTMLFiles/Lorenz_27.gif)
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 10, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_28.gif)
![[Graphics:HTMLFiles/Lorenz_29.gif]](HTMLFiles/Lorenz_29.gif)
![[Graphics:HTMLFiles/Lorenz_32.gif]](HTMLFiles/Lorenz_32.gif)
![[Graphics:HTMLFiles/Lorenz_35.gif]](HTMLFiles/Lorenz_35.gif)
![[Graphics:HTMLFiles/Lorenz_38.gif]](HTMLFiles/Lorenz_38.gif)
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... 1] 0.1, z[1] 0.1, x[1] 0.1}, {x, y, z}, {t, 1, 50}, MaxSteps->100000] ;](HTMLFiles/Lorenz_49.gif)
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 50, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_50.gif)
![[Graphics:HTMLFiles/Lorenz_51.gif]](HTMLFiles/Lorenz_51.gif)
![[Graphics:HTMLFiles/Lorenz_54.gif]](HTMLFiles/Lorenz_54.gif)
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... 2513; -0.1, z[1] -0.1, x[1] -0.1}, {x, y, z}, {t, 1, 50}, MaxSteps->100000] ;](HTMLFiles/Lorenz_56.gif)
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 50, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_57.gif)
![[Graphics:HTMLFiles/Lorenz_58.gif]](HTMLFiles/Lorenz_58.gif)
![NDSolve[{x '[t] σ * (y[t] - x[t]), y '[t] ρ * x[t] - y[t ... ] 0.1, z[1] 0.1, x[1] 0.1}, {x, y, z}, {t, 1, 100}, MaxSteps->100000] ;](HTMLFiles/Lorenz_65.gif)
![Show[Graphics3D[Line[Table[{ (x/.First[%]) [t], (y/. First[%]) [t], (z/. First[%]) [t]}, {t, 1, 100, 0.01}]]], AxesTrue]](HTMLFiles/Lorenz_66.gif)
![[Graphics:HTMLFiles/Lorenz_67.gif]](HTMLFiles/Lorenz_67.gif)
![[Graphics:HTMLFiles/Lorenz_70.gif]](HTMLFiles/Lorenz_70.gif)
![[Graphics:HTMLFiles/Lorenz_73.gif]](HTMLFiles/Lorenz_73.gif)
![[Graphics:HTMLFiles/Lorenz_76.gif]](HTMLFiles/Lorenz_76.gif)
![(f^k(p)) ' = Underoverscript[∏, j = 0, arg3] f ' (f^j(p))](HTMLFiles/Lorenz_94.gif)
![f(x) = α 1 - β | x | ; &n ... ; x∈ (0, 1]](HTMLFiles/Lorenz_117.gif)
![[Graphics:HTMLFiles/Lorenz_122.gif]](HTMLFiles/Lorenz_122.gif)
![[Graphics:HTMLFiles/Lorenz_125.gif]](HTMLFiles/Lorenz_125.gif)
![[Graphics:HTMLFiles/Lorenz_126.gif]](HTMLFiles/Lorenz_126.gif)
![[Graphics:HTMLFiles/Lorenz_128.gif]](HTMLFiles/Lorenz_128.gif)
![[Graphics:HTMLFiles/Lorenz_130.gif]](HTMLFiles/Lorenz_130.gif)
![[Graphics:HTMLFiles/Lorenz_132.gif]](HTMLFiles/Lorenz_132.gif)
![[Graphics:HTMLFiles/Lorenz_134.gif]](HTMLFiles/Lorenz_134.gif)